Interested Article - Счастливое число (lucky number)

Счастли́вое число́ ( англ. lucky number ) в теории чисел — натуральное число из множества, генерируемого «решетом», аналогичным решету Эратосфена , которое генерирует простые числа .

Процесс начинается с полного списка натуральных чисел :

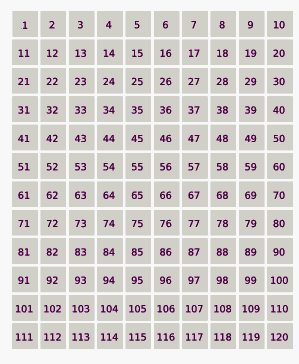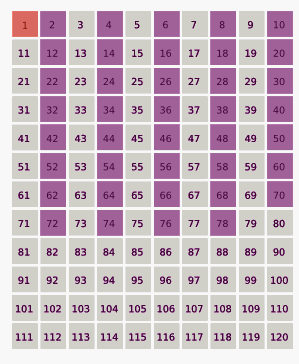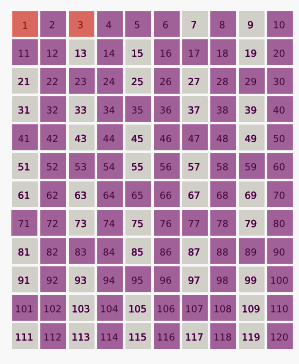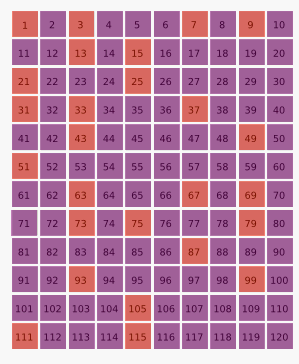
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, …

Каждое второе число (все чётные числа) исключается, остается только нечётные числа:

1,    3,    5,    7,    9,   11,   13,   15,   17,   19,   21,   23,   25,

Второй член в этой последовательности — число 3. Каждое третье число, которое остаётся в списке, исключается:

1,    3,          7,    9,         13,   15,         19,   21,         25,

Теперь третье оставшееся число — 7, поэтому каждый седьмой номер, который остался, исключается:

1,    3,          7,    9,         13,   15,               21,         25,

Процедура постоянно повторяется; остающиеся числа — и есть счастливые числа:

1 , 3 , 7 , 9 , 13 , 15 , 21 , 25 , 31 , 33 , 37 , 43 , , 51 , 63 , , 69 , 73 , , 79 , 87 , , 99 , , , , 127 , 129 , 133 , 135 , 141 , 151 , , 163 , 169 , , , 193 , , , , , , , , , , , , , , , 283 , , , , , , , , , , , , , , , , , , , , , 421 , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , 729 , , , , , , , … (последовательность в OEIS ).

Анимация выявления счастливых чисел. Числа в красных квадратах являются счастливыми числами

История

В 1955 году термин был предложен в работе Гардинера, Лазаруса, Метрополиса и Улама . Также они предложили назвать это решето решетом Иосифа Флавия из-за его схожести с задачей Иосифа Флавия .

Свойства

Счастливые числа по многим свойствам близки к простым числам . Например, их асимптотическая плотность равна ${\dfrac {1}{\ln {n}}},$ то есть совпадает с асимптотической плотностью простых чисел ; счастливые числа-близнецы и простые числа-близнецы также появляются с близкой частотой. Пары счастливых чисел, отличающихся на 4, 6, 8 и т. д., появляются с частотой, близкой к частоте соответствующих пар простых чисел. На счастливые числа может быть распространена версия проблемы Гольдбаха . Существует бесконечное множество счастливых чисел. Из-за этих очевидных связей с простыми числами некоторые математики предположили, что эти свойства могут быть найдены в более широком классе множеств этих чисел, сгенерированных решетом неизвестного вида, хотя теоретические основания для этой гипотезы малы.

Счастливые простые числа

Счастливое простое число — это счастливое число, которое является простым. Неизвестно, бесконечно ли множество счастливых простых чисел. Первые числа этой последовательности:

3 , 7 , 13 , 31 , 37 , 43 , , 73 , 79 , 127 , 151 , 163 , 193 , … (последовательность в OEIS ).

Примечания

V. Gardiner, R. Lazarus, N. Metropolis and S. Ulam, «On certain sequences of integers defined by sieves», Mathematics Magazine 29 :3 (1955), pp. 117—122.
↑ , с. 137-138.

Литература

С. Улам . Нерешённые математические задачи = A Collection of Mathematical Problems / Перевод с английского З. Я. Шапиро . — М. : Наука , 1964. — 168 с. — (Современные проблемы математики).