Звёздчатый многогра́нник ( звёздчатое тело ) — невыпуклый многогранник , грани которого пересекаются между собой. Как и у незвёздчатых многогранников , грани попарно соединяются в рёбрах (при этом внутренние линии пересечения не считаются рёбрами).

Терминология

Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам.

Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые ( конгруэнтные ) правильные или звёздчатые многоугольники . В отличие от пяти классических правильных многогранников ( Платоновых тел ), данные многогранники не являются выпуклыми телами.

В 1811 году Огюстен Лу Коши установил, что существуют всего 4 правильных звёздчатых тела (они называются телами Кеплера — Пуансо ), которые не являются соединениями Платоновых и звёздчатых тел. К ним относятся открытые в 1619 году Иоганном Кеплером малый звёздчатый додекаэдр и большой звёздчатый додекаэдр , а также большой додекаэдр и большой икосаэдр , открытые в 1809 году Луи Пуансо . Остальные правильные звёздчатые многогранники являются или соединениями Платоновых тел, или соединениями тел Кеплера — Пуансо .

Полуправильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются правильные или звёздчатые многоугольники , но не обязательно одинаковые. При этом строение всех вершин должно быть одинаковым (условие однородности). Г. Коксетер , М. Лонге-Хиггинс и Дж. Миллер в 1954 году перечислили 53 таких тела и выдвинули гипотезу о полноте своего списка . Только значительно позже в 1969 году Сопову С. П. удалось доказать, что представленный ими список многогранников действительно полон.

Многие формы звёздчатых многогранников подсказывает сама природа. Например, снежинки — это плоские проекции звёздчатых многогранников. Некоторые молекулы имеют правильные структуры объёмных фигур.

На данных рисунках каждая грань для красоты и наглядности окрашена собственным цветом.

Однородные многогранники — правильные и полуправильные выпуклые многогранники (Платоновы и архимедовы тела); правильные и полуправильные звёздчатые многогранники вместе называются однородными многогранниками. У этих тел все грани являются правильными многоугольниками (выпуклыми или звёздчатыми), а все вершины одинаковы (то есть существуют ортогональные преобразования многогранника в себя, переводящие любую вершину в любую другую). Существует ровно 75 однородных многогранников.

Тетраэдр и куб

Тетраэдр и гексаэдр ( куб ) не имеют звёздчатых форм, так как их грани при продлении через рёбра более не пересекаются.

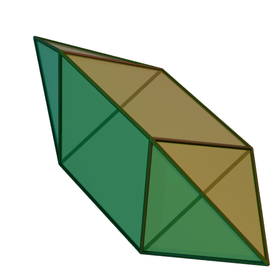
Звёздчатый октаэдр

Существует только одна звёздчатая форма октаэдра . Звёздчатый октаэдр был открыт Леонардо да Винчи , затем спустя почти 100 лет заново открыт И. Кеплером и назван им Stella octangula — звезда восьмиугольная. Отсюда эта форма имеет и второе название: «stella octangula Кеплера»; по сути она является соединением двух тетраэдров.

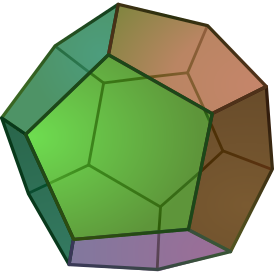
Звёздчатые формы додекаэдра

Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр , большой додекаэдр , большой звёздчатый додекаэдр (звёздчатый большой додекаэдр, завершающая форма). В отличие от октаэдра, любая из звёздчатых форм додекаэдра не является соединением платоновых тел, а образует новый многогранник.

У большого додекаэдра гранями являются пятиугольники, которые сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани — пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3 грани в одной вершине.

Вершины большого звёздчатого додекаэдра совпадают с вершинами описанного додекаэдра.

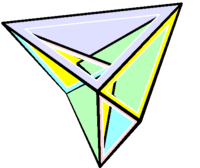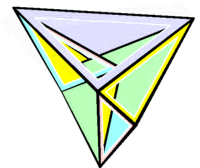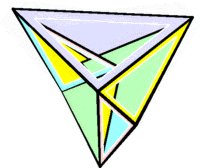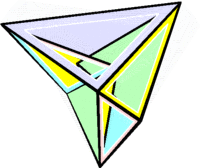
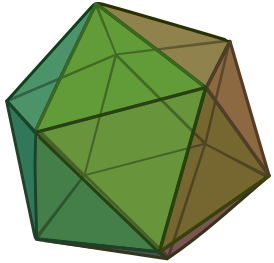
Звёздчатые формы икосаэдра

Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 — неполной икосаэдральной симметрией, что было доказано Коксетером совместно с Дювалем, Флэзером и Петри c применением правил ограничения, установленных Дж. Миллером. Одна из этих звёздчатых форм (20-я, модель 41 по Веннинджеру), называемая большим икосаэдром (см. рисунок), является одним из четырёх правильных звёздчатых многогранников Кеплера — Пуансо . Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.

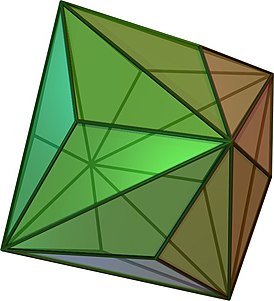
Среди звёздчатых форм также имеются: соединение пяти октаэдров , соединение пяти тетраэдров , . Первая звёздчатая форма — малый триамбический икосаэдр .

Если каждую из граней продолжить неограниченно, то тело будет окружено большим многообразием отсеков — частей пространства, ограниченных плоскостями граней. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20 + 30 + 60 + 20 + 60 + 120 + 12 + 30 + 60 + 60 = 472 отсека десяти различных форм и размеров. Большой икосаэдр состоит из всех этих кусков, за исключением последних шестидесяти. Следующая звёздчатая форма — завершающая.

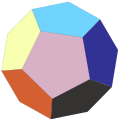
Звёздчатые формы кубооктаэдра

Кубооктаэдр имеет 4 звёздчатые формы, удовлетворяющие ограничениям, введённым Миллером. Первая из них является соединением куба и октаэдра.

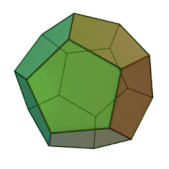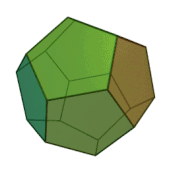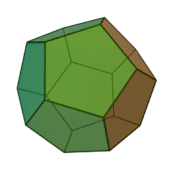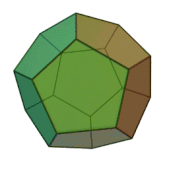
Звёздчатые формы икосододекаэдра

Икосододекаэдр имеет множество звёздчатых форм, первая из которых -- это соединение икосаэдра и додекаэдра.

Икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 — правильными треугольниками.

Приведение к звёздчатой форме

Под приведением к звёздчатой форме понимается процесс построения многогранника из другого многогранника путём расширения его граней. Для этого через грани исходного многогранника проводятся плоскости и рассматриваются всевозможные рёбра, полученные в результате пересечения этих плоскостей, и выбираются подходящие .

Куб и тетраэдр не позволяют приведение к звёздчатой форме. Октаэдр имеет единственное построение — звёздчатый октаэдр . Додекаэдр даёт три звёздчатые формы.

Примечания

Литература

• М. Веннинджер . — М. : Мир, 1974. — 236 с.
• Гончар В. В. . — М. : Аким, 1997. — 64 с. — ISBN 5-85399-032-2 . .
• Гончар В. В. . — Ростов-на-Дону: Феникс, 2010. — 143 с. — ISBN 978-5-222-17061-8 . .
• Сoxeter H. S. M. , Longuet-Higgins M. S., Miller J. C. P. Uniform Polyhedra // Phil. Trans. Roy. Soc. London. Ser. A , 246 . — 1954. — P. 401—450. — doi : .
• Сoxeter H. S. M. . — New York: Dover, 1973. — 321 p. — ISBN 0-486-61480-8 . .
• Сопов С. П. // . — 1970. — Т. 8 . — С. 139—156 . .

Ссылки

• от 26 февраля 2021 на Wayback Machine
• от 25 октября 2020 на Wayback Machine