Interested Article - Звёздчатый октаэдр

Звёздчатый октаэдр , или stella octangula , — единственная звёздчатая форма октаэдра . Латинским именем stella octangula многогранник назвал Кеплер в 1609, хотя он был известен более ранним . Так, он изображён в труде Пачоли De Divina Proportione, 1509.

Многогранник является простейшим из пяти правильных соединений многогранников .

Звёздчатый октаэдр можно рассматривать как трёхмерное обобщение гексаграммы — гексаграмма является двумерной фигурой, образованной двумя наложенными друг на друга правильными треугольниками, центрально симметричными друг другу, и точно таким же образом звёздчатый октаэдр может быть образован из двух центрально симметричных пересекающихся тетраэдров. Его же можно рассматривать как одну из стадий построения 3D- снежинки Коха , фрактальной фигуры, получаемой повторяющимся присоединением меньших тетраэдров к каждой треугольной поверхности большей фигуры. Начальной стадией построения снежинки Коха является один центральный тетраэдр, а второй стадией, полученной добавлением четырёх меньших тетраэдров к граням центрального тетраэдра, и будет звёздчатый октаэдр.

Построение

Звёздчатый октаэдр можно получить несколькими путями:

Это образование звёздчатой формы правильного октаэдра , сохраняющее его плоскости граней. Грани звезды очень простые: (См. модель Веннинджера W ₁₉ ).
Он является правильным соединением многогранников , если строить как объединение двух тетраэдров (тетраэдр и двойственный ему тетраэдр ).
Его можно получить дополнением правильного октаэдра треугольными пирамидами к каждой грани. В этом построении многогранник имеет ту же топологию, что и выпуклое каталаново тело триакисоктаэдр , имеющее куда более короткие пирамиды.
Это огранка куба с сохранением вершин.

Связанные концепции

У представленного в виде сферической мозаики звёздчатого октаэдра рёбра в соединении двух тетраэдров образуют ромбододекаэдр

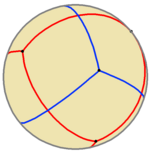
Можно построить соединение двух сферических тетраэдров, как показано на рисунке.

Два тетраэдра в соединении звёздчатого октаэдра являются «десмичными», что означает (если рассматривать их как прямые в проективном пространстве ), что каждое ребро одного тетраэдра пересекает противоположное ребро другого тетраэдра. Одно из таких пересечений видно в звёздчатом октаэдре. Другое пересечение оказывается в бесконечной точке проективной плоскости между двумя параллельными рёбрами двух тетраэдров. Эти два тетраэдра могут быть дополнены до трёх тетраэдров, где третий тетраэдр имеет в качестве чётырёх вершин три точки пересечения на бесконечности и центроид двух конечных тетраэдров. Те же самые двенадцать вершин тетраэдров образуют точки конфигурации Рейе .

124 магнитных шара , расположенные в форме звёздчатого октаэдра

Числа звёздчатого октаэдра — фигурные числа , подсчитывающие число шаров, которые можно расположить внутри звёздчатого октаэдра. Эти числа равны

0, 1, 14 , 51 , 124 , 245, 426, 679, 1016, 1449, 1990, … (последовательность в OEIS )

В популярной культуре

Звёздчатый октаэдр представлен наряду с некоторыми другими многогранниками и соединениями многогранников на картинах Эшера и «Двойной астероид» (1949) .

Галерея

Это полная симметрическая огранка куба

Примечания

.
, с. 59–69.

Литература

P. Cromwell. Polyhedra. — United Kingdom: Cambridge University Press, 1997. — С. 79–86 Archimedean solids . — ISBN 0-521-55432-2 .

H.S.M Coxeter . 3.6 The five regular compounds , pp.47-50, 6.2 Stellating the Platonic solids , pp.96-104 // . — 3rd edition. — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8 .
George W. Hart. The Polyhedra of M.C. Escher // WEB-статья. — 1996.
H. S. M. Coxeter. A special book review: M. C. Escher: His life and complete graphic work // The Mathematical Intelligencer. — 1985. — Т. 7 , вып. 1 . — doi : .