n -угольный осоэдр — мозаика из двуугольников на сферической поверхности, где каждый такой двуугольник имеет две общие вершины (противоположные точки сферы) с другими двуугольниками.

Правильный n-угольный осоэдр имеет символ Шлефли {2, n }, а каждый двуугольник имеет внутренний угол 2π/ n радиан (360/ n градусов .

Осоэдры как правильные многогранники

Для правильных многогранников, символ Шлефли которых равен { m , n }, число многоугольных граней можно найти по формуле:

${\displaystyle N_{2}={\frac {4n}{2m+2n-mn}}}$

Правильные многогранники , известные с античных времён, являются единственными многогранниками, дающими в результате деления целое число для m ≥ 3 и n ≥ 3. Ограничение m ≥ 3 приводит к тому, что многоугольные грани должны иметь по меньшей мере три стороны.

Если рассматривать многогранники как сферическую мозаику , это ограничение может быть ослаблено, поскольку двуугольники можно рассматривать как сферические двуугольные фигуры, имеющие ненулевую площадь . Допущение m = 2 порождает новый бесконечный класс правильных многогранников, то есть осоэдров.

Правильный треугольный осоэдр, {2,3}, представленный в виде мозаики из трёх двуугольников на сфере.

Правильный четырёхугольный осоэдр, представленный в виде мозаики из четырёх двуугольников на сфере.

Семейство правильных осоэдров

n	1	2	3	4	5	6	7	8	9	10	11	12	...
Рисунок
Шлефли	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}	{2,9}	{2,10}	{2,11}	{2,12}
Коксетер
Граней и рёбер	1	2	3	4	5	6	7	8	9	10	11	12
Вершин	2

Калейдоскопическая симметрия

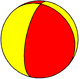
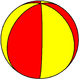
Двуугольные грани 2 n -осоэдра , {2,2n}, представляют фундаментальные области : C _nv , [n], (*nn), порядок 2 n . Области зеркального отражения можно показать, используя поочерёдную раскраску двуугольников. Рассечения двуугольников на два сферических треугольника создают бипирамиды и определяют диэдрическую симметрию D _nh , порядок 4 n .

Симметрия	C 1v	C 2v	C 3v	C 4v	C 5v	C 6v
Осоэдр	{2,2}	{2,4}	{2,6}	{2,8}	{2,10}	{2,12}
Фундаментальные области

Связь с телами Штейнмеца

Четырёхугольный осоэдр топологически эквивалентен бицилиндру , пересечению двух цилиндров под прямым углом .

Производные многогранники

Двойственным многогранником n-угольного осоэдра {2, n } является n -угольный диэдр , { n , 2}. Многогранник {2,2} самодвойственен и является осоэдром и диэдром одновременно.

Осоэдр можно модифицировать тем же способом, что и другие многогранники, порождая варианты. Усечённый n -угольный осоэдр — это n-угольная призма .

Бесконечноугольный осоэдр

В пределе осоэдр становится бесконечноугольным и представляет собой двумерное замощение:

Осотопы

Многомерные аналоги, в общем случае, называются осотопами . Правильный осототоп с символом Шлефли {2,p,…,q} имеет две вершины и в обеих вершинах вершинной фигурой служит {p,…,q}.

Двумерный осотоп ( многоугольник ) {2} — это двуугольник .

Этимология

Термин «осоэдр» (hosohedron) предложен Г. С. М. Коксетером и, возможно, происходит от греческого ὅσος ( осос ) «сколь угодно», что указывает на возможность осоэдра иметь « сколь угодно много граней» .

Однородные шестиугольные диэдральные сферические многогранники

Симметрия : [6,2] , (*622)							[6,2] + , (622)	[6,2 + ], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}		rr{2,6}		sr{6,2}	s{2,6}
Двойственные им многогранники
				V2 6		V4.4.12		V3.3.3.3

* n 32 варианты симметрии правильных мозаик: n ³ или { n ,3}

Сферические				Евклидовы	Компактные гиперболические.		Параком- пактные.	Некомпактные гиперболические.
	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}			{12i,3}	{9i,3}	{6i,3}	{3i,3}

* n 32 мутации симметрий усечённых мозаик: n .6.6
Симметрия	Сферическая		Евклидова	Компактная гиперболическая				Паракомпактная.	Некомпактная гиперболическая
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Усечённые фигуры
Конф.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6				12i.6.6	9i.6.6	6i.6.6
n-кис фигуры
Конф.		V3.6.6	V4.6.6	V5.6.6		V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

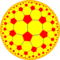
Варианты симметрии * n 42 усечённых мозаик: n .8.8
Симметрия [n,4]	Сферическая		Евклидова	Компактная гиперболич.				Параком- пактная
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Усечённые фигуры
Конфиг.	2.8.8	3.8.8	4.8.8
n-kis фигуры
Конфиг.		V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

Варианты симметрии * n 42 правильных мозаик { n ,4}
Сферические		Евклидовы	Гиперболические мозаики
	3 4	4 4					...

Соты {p,4,4}
Пространство	E 3	H 3
Форма	Аффинные	Паракомпактные		Некмпактные
Название		{3,4,4}				..
Coxeter
Image
Cells		{3,4}	{4,4}

См. также

• Многогранник
• Политоп

Примечания

Литература

• Coxeter H. S. M. . Regular Polytopes. — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8 .
• McMullen, Peter; Schulte, Egon. . Abstract Regular Polytopes. 1st edition. — Cambridge University Press , 2002. — ISBN 0-521-81496-0 .
• Schwartzman, Steven. . . — MAA , 1994. — ISBN 978-0-88385-511-9 .

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .