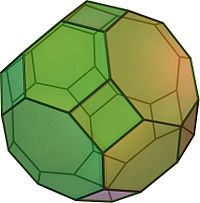
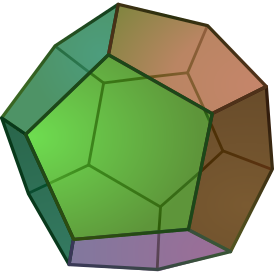
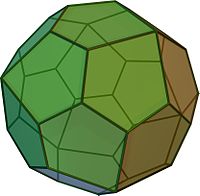
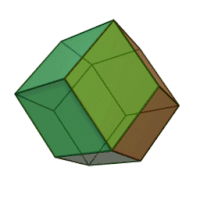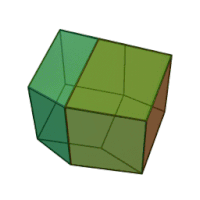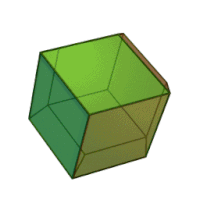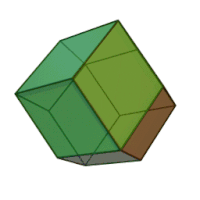
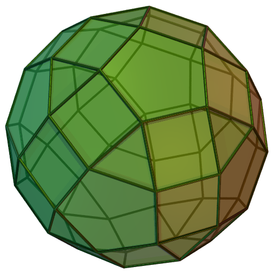
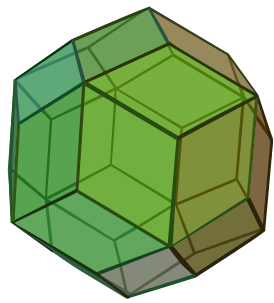
Наращённый усечённый куб — один из многогранников Джонсона ( J ₆₆ , по Залгаллеру — М ₁₁ +М ₅ ).

Составлен из 22 граней: 12 правильных треугольников , 5 квадратов и 5 правильных восьмиугольников . Среди восьмиугольных граней 1 окружена четырьмя восьмиугольными и четырьмя треугольными, остальные 4 — тремя восьмиугольными и пятью треугольными; среди квадратных граней 1 окружена четырьмя квадратными, остальные 4 — квадратной и тремя треугольными; среди треугольных 4 грани окружены тремя восьмиугольными, 4 грани — двумя восьмиугольными и квадратной, остальные 4 — восьмиугольной и двумя квадратными.

Имеет 48 рёбер одинаковой длины. 8 рёбер располагаются между двумя восьмиугольными гранями, 24 ребра — между восьмиугольной и треугольной, 4 ребра — между двумя квадратными, остальные 12 — между квадратной и треугольной.

У наращённого усечённого куба 28 вершин. В 16 вершинах сходятся две восьмиугольных грани и одна треугольная; в 8 вершинах сходятся восьмиугольная, квадратная и две треугольных грани; в 4 вершинах сходятся три квадратных и треугольная грани.

Наращённый усечённый куб можно получить из двух многогранников — усечённого куба и четырёхскатного купола ( J ₄ ), — приложив их друг к другу восьмиугольными гранями.

Метрические характеристики

Если наращённый усечённый куб имеет ребро длины ${\displaystyle a}$ , его площадь поверхности и объём выражаются как

${\displaystyle S=\left(15+10{\sqrt {2}}+3{\sqrt {3}}\right)a^{2}\approx 34{,}3382880a^{2},}$

${\displaystyle V=\left(8+{\frac {16{\sqrt {2}}}{3}}\right)a^{3}\approx 15{,}5424723a^{3}.}$

В координатах

Наращённый усечённый куб можно расположить в декартовой системе координат так, чтобы его вершины имели координаты

• ${\displaystyle (\pm ({\sqrt {2}}-1);\;\pm 1;\;\pm 1),}$
• ${\displaystyle (\pm 1;\;\pm ({\sqrt {2}}-1);\;\pm 1),}$
• ${\displaystyle (\pm 1;\;\pm 1;\;\pm ({\sqrt {2}}-1)),}$
• ${\displaystyle (\pm (2-{\sqrt {2}});\;0;\;3-{\sqrt {2}}).}$
• ${\displaystyle (0;\;\pm (2-{\sqrt {2}});\;3-{\sqrt {2}}).}$

При этом ось симметрии многогранника будет совпадать с осью Oz, а две из четырёх плоскостей симметрии — с плоскостями xOz и yOz.

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .