Изгибаемый многогранник (также непрерывно изгибаемый , нежёсткий ) — многогранник (точнее — многогранная поверхность ), чью пространственную форму можно изменить непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело), а деформация осуществляется только за счёт непрерывного изменения двугранных углов . Такая деформация называется непрерывным изгибанием многогранника.

Примеры

• Первые примеры изгибаемых многогранников были построены бельгийским инженером и математиком Раулем Брикаром в 1897 году . Сейчас их называют октаэдрами Брикара . Они не только невыпуклые, но и имеют самопересечения, что не позволяет построить их движущуюся картонную модель.

• В 1976 году американский математик Роберт Коннелли впервые построил изгибаемый многогранник без самопересечений .

• Из всех известных на сегодняшний день изгибаемых многогранников без самопересечений наименьшее число вершин ( девять ) имеет многогранник, построенный немецким математиком . Многогранник Штеффена можно легко вырезать из бумаги (см. статью).

• Известны примеры изгибаемых многогранников, являющихся реализациями тора или бутылки Клейна или вообще двумерной поверхности любого топологического рода.

• 
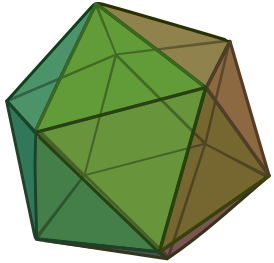
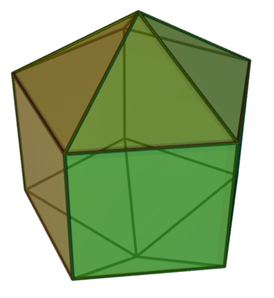
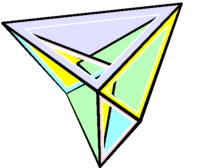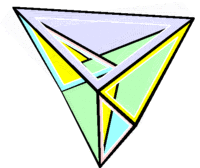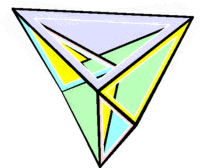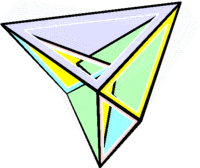
  Изгибаемый октаэдр Брикара первого типа
• 
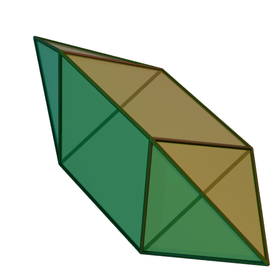
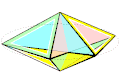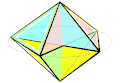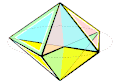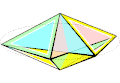  Изгибаемый октаэдр Брикара второго типа
• 
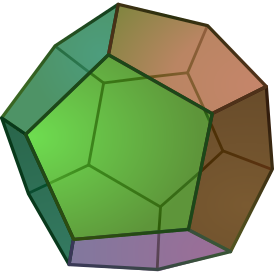
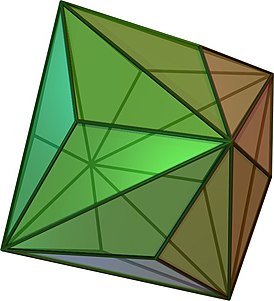
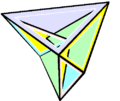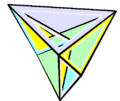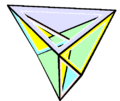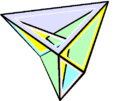  Изгибаемый многогранник Штеффена
• 
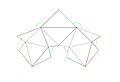  Развёртка изгибаемого многогранника Штеффена

Свойства

В теории изгибаемых многогранников известно немало красивых и нетривиальных утверждений. Ниже приведены наиболее важные из установленных на сегодня фактов:

• Все выпуклые многогранники жёсткие. Это немедленно вытекает из теоремы Коши об однозначной определённости выпуклого многогранника, доказанной в 1813 году .

• Из формулы Шлефли следует, что любой изгибаемый многогранник в процессе изгибания сохраняет так называемую интегральную среднюю кривизну, то есть число, равное ${\displaystyle \sum _{\ell }|\ell |(\pi -\alpha (\ell ))}$ , где ${\displaystyle |\ell |}$ — длина ребра ${\displaystyle \ell }$ , ${\displaystyle \alpha (\ell )}$ — величина внутреннего двугранного угла при ребре ${\displaystyle \ell }$ , а сумма перебирает все рёбра многогранника .

• Теорема Сабитова : любой изгибаемый многогранник в процессе изгибания сохраняет свой объём , то есть он будет изгибаться, даже если его заполнить несжимаемой жидкостью .

• В 2012 году, А. Гайфуллиным доказан многомерный аналог теоремы Сабитова — любой изгибаемый многогранник в размерности ${\displaystyle n\geqslant 4}$ в процессе изгибания сохраняет свой объём.

Вариации и обобщения

Всё сказанное выше относилось к многогранникам в трёхмерном евклидовом пространстве. Однако данное выше определение изгибаемого многогранника примени́мо и к многомерным пространствам и к неевклидовым пространствам, таким как сферическое пространство и пространство Лобачевского . Для них также известны как нетривиальные теоремы, так и открытые вопросы. Например:

• Изгибаемые многогранники существуют во всех размерностях, как в евклидовом пространстве, так и в сферическом и в геометрии Лобачевского. Примеры аналогов изгибаемых октаэдров Брикара в трёхмерной сфере ${\displaystyle S^{3}}$ и в пространстве Лобачевского ${\displaystyle \Lambda ^{3}}$ были построены Штахелем. Первый пример изгибаемого самопересекающегося четырёхмерного многогранника был построен А. Вальц. Наконец, примеры изгибаемых многогранников во всех размерностях и во всех трёх геометриях (евклидовой, сферической, Лобачевского) были построены Гайфуллиным.

• В сферическом пространстве любой размерности существует изгибаемый многогранник, объём которого непостоянен в процессе изгибания. Пример такого самопересекающегося многогранника в размерности 3 был построен в 1997 году Александровым , а пример несамопересекающегося многогранника в сферическом пространстве любой размерности — А. А. Гайфуллиным в его работе 2015 года . Напротив, в трёхмерном пространстве Лобачевского, и вообще в пространстве Лобачевского любой нечётной размерности, объём изгибаемого многогранника обязан сохраняться (так же, как и в евклидовом случае). .

Открытые вопросы

• Верно ли, что многогранник Штеффена имеет наименьшее число вершин среди всех изгибаемых многогранников, не имеющих самопересечений ;

• Верно ли, что если один многогранник, не имеющий самопересечений, получен из другого многогранника, который также не имеет самопересечений, непрерывным изгибанием, то эти многогранники равносоставлены , то есть первый можно разбить на конечное число тетраэдров , каждый из этих тетраэдров независимо от других можно передвинуть в пространстве и получить разбиение второго многогранника .

• В размерностях, начиная с 4, неизвестно, существуют ли изгибаемые несамопересекающиеся многогранники.

• Неизвестно, имеет ли место теорема о кузнечных мехах (должен ли сохраняться объём при изгибании) в пространствах Лобачевского чётной размерности (4, 6,…).

Популярная литература

• В. А. Александров, , Соросовский образовательный журнал . 1997. No. 5. С. 112—117. Та же статья переиздана в книге под редакцией В. Н. Сойфера и Ю. П. Соловьёва: Современное естествознание . Энциклопедия . Т. 3: Математика и механика М.: Наука , М.: Флинта, 2000. ISBN 5-02-004299-4 .
• М. Берже , Геометрия . М.: Мир, 1984. Т. 1. С. 516—517.
• В. А. Залгаллер , , Квант . 1978. No. 9. С. 13—19.
• А. И. Медяник, , Квант . 1979. No. 7. С. 39. (Обратите внимание, что развёртка многогранника Коннелли дана в том же выпуске журнала на оборотной стороне .)
• И.Х. Сабитов,. . — М.: МЦНМО , 2002. — 32 с.
• . Математический цветник. Сборник статей и задач = The Mathematical Gardner / Пер. с англ. Ю. А. Данилова ; под ред., с предисл. и прилож. И. М. Яглома . — М. : Мир, 1983. — С. 105—117. — 494 с.
• Лекция 25 в Табачников С.Л.. Фукс Д.Б. . — МЦНМО, 2011. — 512 с. — 2000 экз. — ISBN 978-5-94057-731-7 .
• Фильм « », сайт Математические этюды
• на YouTube

Научная литература

• В. А. Александров, , Сиб. мат. журн. 1995. Т. 36, No 6. С. 1215—1224.
• Н. Х. Кёйпер , Изгибаемые полиэдральные сферы в ${\displaystyle E^{3}}$ , по Роберту Коннелли , в кн. под ред. А. Н. Колмогорова и С. П. Новикова : Исследования по метрической теории поверхностей. М.: Мир. 1980. С. 210—227.
• P. Коннелли , Об одном подходе к проблеме неизгибаемости . Там же. С. 164—209.
• Р. Коннелли , Некоторые предположения и нерешённые вопросы в теории изгибаний . Там же. С. 228—238.
• И. Г. Максимов, , Фундам. прикл. матем. 2006. Т. 12, No. 1. С. 143—165.
• С. Н. Михалёв, Некоторые необходимые метрические условия изгибаемости подвесок , Вестник МГУ, Сер. I, 2001, No. 3, 15—21.
• И. Х. Сабитов , , Фундам. прикл. матем. 1996. Т. 2, No. 4. С. 1235—1246.
• И. Х. Сабитов , Обобщённая и некоторые её следствия , Матем. сб. 1998. Т. 189, No. 10. С. 105—134.

Примечания