Interested Article - Цифровой водяной знак

Пример цифрового водяного знака (слева нормальное изображение, справа помеченное, в центре разница между изображениями с увеличенной яркостью)

Цифровой водяной знак (ЦВЗ) — технология, созданная для защиты авторских прав мультимедийных файлов. Обычно цифровые водяные знаки невидимы. Однако ЦВЗ могут быть видимыми на изображении или видео. Обычно это информация представляет собой текст или логотип , который идентифицирует автора.

Невидимые ЦВЗ внедряются в цифровые данные таким образом, что пользователю трудно выявить добавленную метку, если он не знаком с её форматом. Например, если водяной знак нужно нанести на графическое изображение , то данная процедура может быть сделана с помощью изменения яркости определённых точек. Если модификация яркости незначительна, то при просмотре рисунка человек, скорее всего, не заметит следов искусственного преобразования. Особенно хорошо данная техника работает в случае, когда водяной знак наносится на неоднородные области — например, на участок фотографии, где изображена трава.

Важнейшее применение цифровые водяные знаки нашли в системах защиты от копирования, которые стремятся предотвратить или удержать от несанкционированного копирования цифровых данных. Стеганография применяет ЦВЗ, когда стороны обмениваются секретными сообщениями, внедрёнными в цифровой сигнал. Используется как средство защиты документов с фотографиями — паспортов, водительских удостоверений, кредитных карт с фотографиями. Комментарии к цифровым фотографиям с описательной информацией — ещё один пример невидимых ЦВЗ. Хотя некоторые форматы цифровых данных могут также нести в себе дополнительную информацию, называемую метаданные , ЦВЗ отличаются тем, что информация «зашита» прямо в сигнал. Объекты мультимедиа в этом случае будут представлять собой контейнеры (носители) данных. Основное преимущество состоит в наличии условной зависимости между событием подмены объекта идентификации и наличии элемента защиты — скрытого водяного знака. Подмена объекта идентификации приведёт к выводу о подделке всего документа. Цифровые водяные знаки получили своё название от старого понятия водяных знаков на бумаге (деньгах, документах).

Применение

Отслеживание распространения копий данных .
- борьба с видеопиратством и «ранний» доступ к новинкам кино: при сотрудничестве с киностудиями Голливуда операторы телевизионных сетей могут предоставлять своим зрителям платный доступ к премиум-контенту — фильмам, только что появившимся в кинотеатрах и ещё не вышедшим на DVD . Обязательным условием студий при этом является встраивание водяного знака, позволяющего обнаружить источник утечки — конкретного зрителя — при попадании фильма в нелегальный оборот .
- отслеживание трансляций ( телевизионные новости часто содержат водяные знаки, оставленные международными информационными агентствами ; рекламные агентства используют водяные знаки для контроля выхода своей рекламы в эфир в оговоренном объёме).
Метаданные , электронная цифровая подпись
Сокрытие факта обмена информации ( стеганография ).

Жизненный цикл цифровых водяных знаков

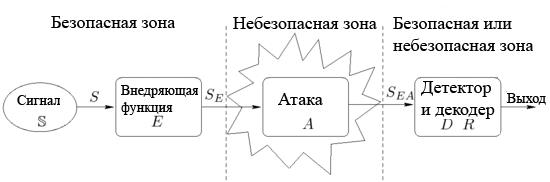
Так называемый, жизненный цикл ЦВЗ может быть описан следующим образом. Сначала в сигнал-источник $S$ $S$ в доверенной среде внедряются водяные знаки при помощи функции $E$ $E$ . В результате получается сигнал $S_{E}$ $S_{E}$ . Следующий этап — распространение $S_{E}$ $S_{E}$ через сеть или любым другим способом. Во время распространения на сигнал может быть совершена атака. У получившегося сигнала $S_{EA}$ $S_{EA}$ водяные знаки могут быть потенциально уничтожены или изменены. На следующем этапе функция обнаружения $D$ $D$ пытается обнаружить водяные знаки $w$ $w$ , а функция $R$ $R$ вытащить из сигнала внедрённое сообщение. Этот процесс потенциально может совершать злоумышленник.

Свойства цифровых водяных знаков

Обычно ЦВЗ классифицируются по 7 основным параметрам: объём, сложность, обратимость, прозрачность, надёжность, безопасность и верификация.

Объём информации

Различают внедряемый и извлекаемый объём.

Внедряемый объём

Внедряемый объём — это просто размер сообщения $m$ $m$ , которое внедряется в сигнал. Её можно определить как: ${\text{cap}}_{E}(S)={\text{size(M)}}=|M|$ ${\text{cap}}_{E}(S)={\text{size(M)}}=|M|$ Рассматривается также относительный внедряемый объём: ${{\text{cap}}_{E}}_{\text{rel}}(S)={\frac {{\text{cap}}_{E}}{{\text{size}}(S)}}.$ ${{\text{cap}}_{E}}_{\text{rel}}(S)={\frac {{\text{cap}}_{E}}{{\text{size}}(S)}}.$

Извлекаемый объём

Извлекаемый объём — это количество информации $m'$ $m'$ извлечённое из сообщения. В случае, если целью ЦВЗ не является передача информации, то извлекаемая информация равна нулю. Для не пустых сообщений извлекаемый объём считается после извлечения. Она считается по следующей формуле: ${{\text{cap}}_{R}}_{\text{rel}}(S_{EA})=|m|-\sum _{i=1}^{|m|}m_{i}\oplus m'_{i}$ ${{\text{cap}}_{R}}_{\text{rel}}(S_{EA})=|m|-\sum _{i=1}^{|m|}m_{i}\oplus m'_{i}$ , где $m=m_{1}m_{2}\dots m_{|m|}$ $m=m_{1}m_{2}\dots m_{|m|}$ , $m'=m'_{1}m'_{2}\dots m'_{|m|}$ $m'=m'_{1}m'_{2}\dots m'_{|m|}$ и $\oplus$ $\oplus$ обозначает исключающее или. Это функция количества корректно переданных бит, она предполагает, что оба сообщения имеют одну длину. Иногда, сообщение повторяют в сигнале несколько раз. В этом случае извлекаемое сообщение в несколько раз длиннее исходного. Следующее выражение учитывает это $p_{\max }$ $p_{\max }$ повторений: ${{\text{cap}}_{R}^{*}}_{\text{rel}}(S_{EA})=\sum _{j=1}^{p_{\max }}\left[|m|-\sum _{i=1}^{|m|}m_{i}\oplus m'_{ji}\right].$ ${{\text{cap}}_{R}^{*}}_{\text{rel}}(S_{EA})=\sum _{j=1}^{p_{\max }}\left[|m|-\sum _{i=1}^{|m|}m_{i}\oplus m'_{ji}\right].$ Объём обычно нормируется на длину сообщения. Рассматриваются иногда такие параметры как ёмкость в секунду и ёмкость, отнесённая к $p_{\max }$ $p_{\max }$ : ${{\text{cap}}_{R}^{\$}}_{\text{rel}}(S_{EA})={\frac {{{\text{cap}}_{R}^{*}}_{\text{rel}}(S_{EA})}{|m|p_{\max }}}.$ ${{\text{cap}}_{R}^{\$}}_{\text{rel}}(S_{EA})={\frac {{{\text{cap}}_{R}^{*}}_{\text{rel}}(S_{EA})}{|m|p_{\max }}}.$

Сложность

Сложность заданной функции $F$ $F$ всегда может быть измерена. Любые затраченные усилия на внедрение, атаку, детектирование или расшифровку измеряются сложностью. Пусть $C(F)$ $C(F)$ to измеряет сложность $F$ $F$ . За $C(E,S)$ $C(E,S)$ обозначим сложность процесса внедрения информации в сигнал $S$ $S$ . В зависимости от реализации функция $C$ $C$ измеряет затрачиваемое время количество операций ввода-вывода , количество строк кода и т. д. Сложность зависит от сигнала $S$ $S$ . Поэтому часто рассматривается нормированная функция независящая от $S$ $S$ . Нормализация может проводиться как по длине $\mathrm {size} (S)$ $\mathrm {size} (S)$ (измеряемой например, в секундах, или битах) сигнала так и по внедряемому объёму:

 ${\text{com}}_{\text{rel}}^{S}(S)={\frac {{\text{com}}_{\text{rel}}^{*}}{\mathrm {size} (S)}}={\frac {C(E,S)}{\mathrm {size} (S)}}$  ${\text{com}}_{\text{rel}}^{S}(S)={\frac {{\text{com}}_{\text{rel}}^{*}}{\mathrm {size} (S)}}={\frac {C(E,S)}{\mathrm {size} (S)}}$

Заметим, что здесь предполагается линейная зависимость $C(E,S)$ $C(E,S)$ от $S$ $S$ . В нелинейном случае можно нормировать на внедрённый объём:

 ${\text{com}}_{\text{rel}}^{C}(S)={\frac {{\text{com}}_{\text{rel}}^{*}}{{\text{cap}}_{E}^{*}}}={\frac {C(E,S)}{{\text{cap}}_{E}^{*}}}$  ${\text{com}}_{\text{rel}}^{C}(S)={\frac {{\text{com}}_{\text{rel}}^{*}}{{\text{cap}}_{E}^{*}}}={\frac {C(E,S)}{{\text{cap}}_{E}^{*}}}$

Оба определения рассматривают конкретный сигнал $S$ $S$ . Рассматриваются также следующие параметры ЦВЗ:

Средняя сложность, нормированная на длину сигнала или объём: ${\text{com}}_{\text{av}}^{S}={\frac {1}{|\mathbb {S} |}}{\sum _{S\in \mathbb {S} }{\text{com}}_{\text{rel}}^{S}(S)}$ ${\text{com}}_{\text{av}}^{S}={\frac {1}{|\mathbb {S} |}}{\sum _{S\in \mathbb {S} }{\text{com}}_{\text{rel}}^{S}(S)}$ ; ${\text{com}}_{\text{av}}^{C}={\frac {1}{|\mathbb {S} |}}{\sum _{S\in \mathbb {S} }{\text{com}}_{\text{rel}}^{C}(S)}$ ${\text{com}}_{\text{av}}^{C}={\frac {1}{|\mathbb {S} |}}{\sum _{S\in \mathbb {S} }{\text{com}}_{\text{rel}}^{C}(S)}$
Максимальная сложность, нормированная на длину сигнала или объём: ${\text{com}}_{\text{mx}}^{S}=\max _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{S}(S)\right\}$ ${\text{com}}_{\text{mx}}^{S}=\max _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{S}(S)\right\}$ ; ${\text{com}}_{\text{mx}}^{C}=\max _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{C}(S)\right\}$ ${\text{com}}_{\text{mx}}^{C}=\max _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{C}(S)\right\}$
Минимальная сложность, нормированная на длину сигнала или объём: ${\text{com}}_{\text{mn}}^{S}=\min _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{S}(S)\right\}$ ${\text{com}}_{\text{mn}}^{S}=\min _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{S}(S)\right\}$ ; ${\text{com}}_{\text{mn}}^{C}=\min _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{C}(S)\right\}$ ${\text{com}}_{\text{mn}}^{C}=\min _{S\in \mathbb {S} }\left\{{\text{com}}_{\text{rel}}^{C}(S)\right\}$

Обратимость

Технология предполагает возможность удалить ЦВЗ $w$ $w$ из помеченного сигнала $S_{E}$ $S_{E}$ . Если полученный сигнал $S'$ $S'$ совпадает с исходным $S=S'$ $S=S'$ , то говорят об обратимости. Возможность обратить предоставляется специальными алгоритмами. Эти алгоритмы используют секретные ключи для защиты от несанкционированного доступа к контенту.

Прозрачность

По данным эталонному $S_{\text{ref}}$ $S_{\text{ref}}$ и тестовому $S_{\text{test}}$ $S_{\text{test}}$ сигналам, функция прозрачности Т измеряет расхождение между этими сигналами $T(S_{\text{ref}},S_{\text{test}})$ $T(S_{\text{ref}},S_{\text{test}})$ . Результат вычисления заключён в интервале [0,1], где 0 соответствует случаю, когда система не может распознать в $S_{\text{test}}$ $S_{\text{test}}$ версию $S_{\text{ref}}$ $S_{\text{ref}}$ , и 1, если наблюдатель не может отличить эти два сигнала.

Надёжность

В этом разделе описывается надёжность ЦВЗ. Сначала надо ввести понятие «успешного обнаружения».

Успешное обнаружение

Для измерения успеха функций обнаружения и дешифровки вводится функция «успешного обнаружения». Для ЦВЗ без закодированного сообщения ${\text{det}}_{D}$ ${\text{det}}_{D}$ D возвращает 0, если водяные знаки не могут быть обнаружены и $1$ $1$ иначе, как в следующей формализации: ${\text{det}}_{D}(S_{EA})={\begin{cases}0,{\text{negative}},\\1,{\text{positive.}}\end{cases}}$ ${\text{det}}_{D}(S_{EA})={\begin{cases}0,{\text{negative}},\\1,{\text{positive.}}\end{cases}}$ Для того чтобы измерить количество успешных внедрений по нескольким тестам $\mathbb {S}$ $\mathbb{S}$ , средняя ${\text{det}}_{D}$ ${\text{det}}_{D}$ может быть вычислена следующем образом: ${{\text{det}}_{D}}_{\text{av}}={\frac {1}{|{\mathbb {S} }|}}\sum _{S\in \mathbb {S} }{\text{det}}_{D}$ ${{\text{det}}_{D}}_{\text{av}}={\frac {1}{|{\mathbb {S} }|}}\sum _{S\in \mathbb {S} }{\text{det}}_{D}$ . Для схем с ненулевым внедрённым сообщением важно знать, что хотя бы одно (в случае множественного внедрения) сообщение расшифровалось успешно. Если, к примеру, сообщение $m$ $m$ внедряется $\left(p_{\max }\right)$ $\left(p_{\max }\right)$ раз, и извлечённый объём ${{\text{cap}}_{R}^{*}}_{\text{rel}}$ ${{\text{cap}}_{R}^{*}}_{\text{rel}}$ returns, на 10 % восстановима, то непонятно, какие именно из $m_{i}$ $m_i$ сообщений повреждены. Тем не менее, такое определение бывает полезным, если знать, что хотя бы одно из сообщений не повредилось, что отражено в следующем выражении: ${\text{det}}_{R}(S_{EA})={\begin{cases}1,\exists j\in \displaystyle \left\{1,\dots ,p_{\max }\right\}:\sum _{i=1}^{|m|}m'_{ji}\oplus m_{ji}=0,\\0,{\text{otherwise}}.\end{cases}}$ ${\text{det}}_{R}(S_{EA})={\begin{cases}1,\exists j\in \displaystyle \left\{1,\dots ,p_{\max }\right\}:\sum _{i=1}^{|m|}m'_{ji}\oplus m_{ji}=0,\\0,{\text{otherwise}}.\end{cases}}$ Отметим, что это не единственное возможное определение. Например, определение может быть следующем: ${\text{det}}_{R\tau }(S_{EA})={\begin{cases}1,{\text{if }}{{\text{cap}}_{R}^{\$}}_{\text{rel}}({\tilde {S}})\geq \tau ,\\0,{\text{otherwise}}.\end{cases}}$ ${\text{det}}_{R\tau }(S_{EA})={\begin{cases}1,{\text{if }}{{\text{cap}}_{R}^{\$}}_{\text{rel}}({\tilde {S}})\geq \tau ,\\0,{\text{otherwise}}.\end{cases}}$ то есть детекция успешна тогда, когда количество успешно извлечённых бит выше некоторого предела $\tau$ $\tau$ (который равен или близок к 1).

Надёжность ЦВЗ

Мера надёжности ${\text{rob}}_{\text{rel}}$ ${\text{rob}}_{\text{rel}}$ ЦВЗ — это число, заключённое в интервале $[0,1]$ $[0,1]$ , где 0 наихудшее возможное значение и 1 наилучшее. Для измерения надёжности используются понятия числа ошибочных байтов и частоты ошибочных битов. Измеряется расстояние между строками извлечённого и внедрённого сообщений или процент совпадений для побитового сравнения. Если строки совпадают, то метод надёжен. ЦВЗ схема считается ненадёжной, если более чем $\nu$ $\nu$ бит повреждены и прозрачность атак выше чем $\tau$ $\tau$ . Например, для ЦВЗ, подверженный атакам $S_{EA}=A_{i,j}(S_{E})$ $S_{EA}=A_{i,j}(S_{E})$ , с сообщением может быть вычислена следующем образом: ${\text{rob}}_{\text{rel}}^{byte}(S_{E})=1-\max _{A_{i,j}\in {\mathcal {A}}}\left\{T\left(S_{E},S_{EA}\right):{\text{det}}_{R}\left(S_{EA},[S,m]\right)=0\right\}$ ${\text{rob}}_{\text{rel}}^{byte}(S_{E})=1-\max _{A_{i,j}\in {\mathcal {A}}}\left\{T\left(S_{E},S_{EA}\right):{\text{det}}_{R}\left(S_{EA},[S,m]\right)=0\right\}$ Индекс $byte$ $byte$ указывает на то, что вычисляется количество ошибочных байт. Для ЦВЗ без сообщения нет извлекающей функции, поэтому методы вычисления ошибочных бит и байт не применимы. Функция надёжности оценивает худший случай. При оценке надёжности любой системы, за меру надёжности принимают надёжность самого ненадёжного звена системы, в случае самой сильной атаки. В данном случае под худшей атакой понимается атака, при которой ЦВЗ удаляется без потери качества сигнала.

Безопасность

Описывает устойчивость ЦВЗ по отношению к определённым атакам.

Верификация

Определяет тип дополнительной информации необходимой функции обнаружения/извлечения для работы.

Необходим исходный сигнал S.
Необходимо внедряемое сообщение m и некоторая дополнительная информация, кроме исходного сигнала.
Нет необходимости в дополнительной информации.

Классификация

ЦВЗ называют надёжным по отношению к классу преобразований Т, если информации из помеченного сигнала можно доверять даже после воздействия на него ухудшения из Т. Типичные преобразования изображения: JPEG компрессия, поворот, обрезание, добавление шума и т. д. Для видео контента к этому списку добавляется MPEG компрессия и временные преобразования. ЦВЗ называют незаметным , если исходный и помеченный сигналы по определённым критериям восприятия неотличимы. Обычно легко сделать надёжный или незаметный ЦВЗ. Но, как правило, тяжело сделать ЦВЗ незаметный и надёжный одновременно.

Технологии ЦВЗ могут быть классифицированы различными способами.

Надёжность

ЦВЗ называется хрупким , если при малейшей модификации его уже нельзя обнаружить. Такие ЦВЗ обычно используют для проверки целостности.

ЦВЗ называется полухрупким , если он выдерживает незначительные модификации сигнала, но вредоносные преобразования не выдерживает. Полухрупкие ЦВЗ используются обычно для обнаружения атаки на сигнал.

ЦВЗ называется надёжным , если он противостоит всем известным видам атак. Такие ЦВЗ обычно используются в системах защиты от копирования и идентификации.

Объём

Длина внедряемого сообщения $|m|$ $|m|$ определяет две различные схемы ЦВЗ:

$|m|=0$ $|m|=0$ : Сообщение $m$ $m$ концептуально нулевое. Задача системы лишь зафиксировать присутствие водяного знака $w$ $w$ в помеченном объекте $S_{E}$ $S_{E}$ . Иногда, такой тип ЦВЗ называют 1-битным водяным знаком, так как 1 отвечает за присутствие знака, а 0 за отсутствие.
$|m|=n>0$ $|m|=n>0$ : Сообщение $m$ $m$ в виде n-битного числа ( $m=m_{1}\ldots m_{n},\;n\in \mathbb {N}$ $m=m_{1}\ldots m_{n},\;n\in \mathbb {N}$ , with $n=|m|$ $n=|m|$ ) или $M=\{0,1\}^{n}$ $M=\{0,1\}^{n}$ зашито в $w$ $w$ . Это обычная схема ЦВЗ с ненулевым сообщением.

Метод нанесения ЦВЗ

Методы нанесения ЦВЗ делятся на пространственные и частотные. К пространственным методам относится . К частотным - методом расширения спектра . Помеченный сигнал получается аддитивной модификацией. Такие ЦВЗ отличаются средней надёжностью, но очень маленьким информационной ёмкостью. Метод амплитудной модуляции , схожий с методом расширения спектра, также применяется для внедрения. Метод квантования не очень надёжен, но позволяет внедрить большой объём информации.