Interested Article - Квадратный паркет

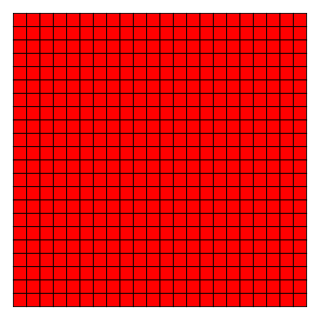
Квадратная мозаика

Тип
Конфигурация граней	4.4.4.4 (или 4 ⁴ ) \|
Конфигурация граней	V4.4.4.4 (или V4 ⁴ )
Символ Шлефли	{4,4} $\{\infty \}\times \{\infty \}$
	4 \| 2 4
Диаграммы Коксетера — Дынкина
Симметрия	p4m , [4,4], (*442)
Симметрия вращения	], p4 , [4,4] ⁺ , (442)\|
Двойственная мозаика	самодвойственны
Свойства	вершинно транзитивная гране транзитивная рёберно транзитивная

Квадра́тный парке́т , квадратный паркетаж , квадратная мозаика или квадратная решётка — это замощение плоскости равными квадратами , расположенными сторона к стороне, при этом вершины четырёх смежных квадратов находятся в одной точке. Символ Шлефли мозаики — {4,4}, означающий, что вокруг каждой вершины имеется 4 квадрата .

Конвей называл эту мозаику quadrille (кадриль).

Внутренний угол квадрата составляет 90 градусов, так что четыре квадрата в вершине дают полный угол в 360 градусов. Мозаика является одной из трёх правильных мозаик на плоскости . Другие две — треугольная мозаика и шестиугольная мозаика .

Однородные раскраски

Существует 9 различных однородных раскрасок квадратной мозаики. Цвета 4 квадратов по индексам цвета вокруг вершины: 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234. Помечены через (i) случаи с простой зеркальной симметрией и через (ii) случаи со скользящей зеркальной симметрией. Три из этих вариантов можно рассматривать в той же фундаментальной области как редуцированные раскраски — 1112 _i получается из 1213, 1123 _i из 1234, а 1112 _ii из 1123 _ii .

9 однородных раскрасок
1111	1212	1213	1112 _i	1122

p4m (*442)		p4m (*442)		pmm (*2222)
1234	1123 _i	1123 _ii	1112 _ii

pmm (*2222)		cmm (2*22)

Шахматная раскраска (цвета 1212) является основой для многих игр и головоломок, например, поле шахматной доски представляет собой квадратный паркет, также и для многих других , кроссвордов , полимино , модели «Жизнь» и других двумерных клеточных автоматов и т. п.

Доска одного цвета (цвета 1111) используется, например, в игре Го .

Связанные многогранники и мозаики

Эта мозаика топологически является частью последовательности правильных многогранников и мозаик, продолжающейся в гиперболической плоскости : {4,p}, p=3,4,5…

Варианты симметрии * n 42 правильных мозаик: {4, n }
Сферические	Евклидовы	Компактные гиперболические				Паракомпактные
{4,3}					...

Квадратная мозаика являются частью последовательности правильных многогранников и мозаик, имеющих четыре грани на вершину. Последовательность начинается с октаэдра , символы Шлефли последовательности — {n,4}, а диаграммы Коксетера — при n, стремящемся к бесконечности.

Варианты симметрии * n 42 правильных мозаик { n ,4}
Сферические		Евклидовы	Гиперболические мозаики

2 ⁴	3 ⁴			...

Варианты симметрии * n 42 квазиправильных двойственных мозаик: V (4.n) ²
Симметрия *4n2 [n,4]	Сферические	Евклидовы	Компактные гиперболические				Паракомпактные	Некомпактные
Симметрия *4n2 [n,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[iπ/λ,4]
Мозаика Конф.	V4.3.4.3			V4.6.4.6	V4.7.4.7	V4.8.4.8	V4.∞.4.∞	V4.∞.4.∞

Варианты симметрии * n 42 расширенных мозаик: n .4.4.4
Симметрия [n,4], (* n 42)	Сферические	Евклидовы	Компактные гиперболические				Паракомпактные
Симметрия [n,4], (* n 42)	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]	*∞42 [∞,4]
Расширенные тела
Конфиг.	3.4.4.4
Ромбические тела конфиг.	V3.4.4.4		V5.4.4.4	V6.4.4.4	V7.4.4.4	V8.4.4.4	V∞.4.4.4

Построение Витхоффа из квадратной мозаики

Подобно однородным многогранникам существует восемь , имеющих в основе правильную квадратную мозаику.

Рисуя оригинальные грани красным цветом, оригинальные вершины жёлтым, а оригинальные рёбра синим, получим 8 различных мозаик. Однако существует только три топологически различных мозаики — квадратная мозаика , усечённая квадратная мозаика и плосконосая квадратная мозаика .

Однородные мозаики на основе симметрии квадратной мозаики
Симметрия : [4,4], (*442)				[4,4] ⁺ , (442)	[4,4 ⁺ ], (4*2)


	t{4,4}	t{4,4}	tr{4,4}	sr{4,4}	s{4,4}
Uniform duals


	V4.8.8	V4.8.8	V4.8.8	V3.3.4.3.4

Топологически эквивалентные мозаики

Изогональный вариант с двумя типами граней

2-изоэдральный вариант с ромбическими гранями

Другие четырёхугольные мозаики могут быть топологически эквивалентны квадратным мозаикам (4 четырёхугольника при каждой вершине).

Изоэдральные мозаики имеют одинаковые грани ( транзитивность по граням ) и они вершинно транзитивны . Имеется 18 вариантов, при этом 6 имеют треугольные грани, не соединяющиеся ребро-к-ребру, и ещё 6 состоят из четырёхугольников с двумя параллельными рёбрами (трапеций). Приведённая симметрия предполагает, что все грани выкрашены в один цвет .

Изоэдральные четырёхугольные мозаики
Квадрат p4m, (*442)	Прямоугольник pmm, (*2222)	Параллелограмм p2, (2222)	Параллелограмм pmg, (22*)	Ромб cmm, (2*22)


Трапеция cmm, (2*22)	Четырёхугольник pgg, (22×)	Дельтоид pmg, (22*)	Четырёхугольник pgg, (22×)	Четырёхугольник p2, (2222)

Вырожденные четырёхугольники или треугольники, не соприкасающиеся ребро-к-ребру
Равнобедренный pmg, (22*)	Равнобедренный pgg, (22×)		Неравносторонний pgg, (22×)		Неравносторонний p2, (2222)

Упаковка кругов

Квадратную мозаику можно использовать для упаковки кругов , если размещать круги одинакового диаметра с центрами в вершинах квадратов. Каждый круг соприкасается с четырьмя другими кругами упаковки ( контактное число ) . Плотность упаковки равна $\pi /4\approx 78{,}54\%$ . Существует 4 однородных раскраски упаковки кругов.

Связанные правильные комплексные бесконечноугольники

Существует 3 правильных комплексных апейрогона , имеющих те же вершины, что и квадратная мозаика. Правильные комплексные апейрогоны имеют вершины и рёбра, при этом рёбра могут содержать 2 и более вершин. Правильные апейрогоны p{q}r ограничены выражением 1/ p + 2/ q + 1/ r = 1. Здесь предполагается, что рёбра содержат p вершин, а вершинная фигура r -гональна .

Самодвойственные	Двойственные

4{4}4 или	2{8}4 или	4{8}2 или

См. также

Примечания

, с. 147.
, с. 473—481.
, с. 74—75.
, с. 111—112, 136.

Литература

Голомб С. В. = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М. : Мир, 1975. — 207 с.
Coxeter H. C. M. Table II: Regular honeycombs // . — Third edition. — Dover Edition, 1973. — С. . — ISBN 0-486-61480-8 .
Klitzing, Richard от 9 декабря 2017 на Wayback Machine
Williams, R. . — New York: Dover Publications , 1979. — С. . — ISBN 0-486-23729-X .
Branko Grünbaum , G. C. Shephard. . — W. H. Freeman, 1987. — С. 58—65 (Chapter 2.1: Regular and uniform tilings). — ISBN 0-7167-1193-1 .
John H. Conway , Heidi Burgiel, Chaim Goodman-Strass. . — Wellesley, MA: A K Peters, Ltd., 2008. — ISBN 978-1-56881-220-5 . от 19 сентября 2010 на Wayback Machine
Keith Critchlow. Order in Space: A design source book. — New York: Thames & Hudson, 1987. — С. 77—76, pattern 8. — ISBN 0-500-34033-1 .