Interested Article - B⁺-дерево

Простой пример $B^{+}$ $B^{+}$ дерева, связывающего ключи 1—7 с данными $d_{1}-d_{7}.$ $d_{1}-d_{7}.$ Указатели связанного списка (помечены красным) позволяют быстро перемещаться по элементам по порядку. Параметр ветвления этого конкретного дерева $b=4$ $b=4$ .

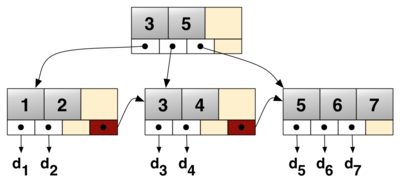
B⁺-дерево — структура данных на основе B-дерева , сбалансированное $n$ $n$ -арное дерево поиска с переменным, но зачастую большим количеством потомков в узле. B⁺-дерево состоит из корня, внутренних узлов и листьев, корень может быть либо листом, либо узлом с двумя и более потомками.

Изначально структура предназначалась для хранения данных в целях эффективного поиска в блочно-ориентированной среде хранения — в частности, для файловых систем; применение связано с тем, что в отличие от бинарных деревьев поиска, B⁺-деревья имеют очень высокий коэффициент ветвления (число указателей из родительского узла на дочерние — обычно порядка 100 или более), что снижает количество операций ввода-вывода, требующих поиска элемента в дереве.

Вариант B⁺-дерева, в котором все значения сохранялись в листовых узлах, систематически рассмотрен в 1979 году , притом отмечено, что такие структуры использовались IBM в технологии файлового доступа для мейнфреймов по крайней мере с 1973 года.

Структура широко применяется в файловых системах — NTFS , ReiserFS , NSS , XFS , JFS , ReFS и BFS используют этот тип дерева для индексирования метаданных; BeFS также использует B⁺-деревья для хранения каталогов. Реляционные системы управления базами данных , такие как DB2 , Informix , Microsoft SQL Server , Oracle Database (начиная с версии 8), Adaptive Server Enterprise и SQLite поддерживают этот тип деревьев для табличных индексов. Среди NoSQL -СУБД, работающих с моделью «ключ—значение», структура данных реализована для доступа к данным в CouchDB , MongoDB (при использовании подсистемы хранения WiredTiger ) и .

Описание

B⁺-деревом называется сбалансированное $n$ $n$ -арное дерево поиска порядка (или степени) $t,$ $t,$ удовлетворяющее следующим свойствам:

Каждый узел содержит хотя бы один ключ; ключи в каждом узле упорядочены, корень содержит от $1$ $1$ до $2t-1$ $2t-1$ ключей, любой другой узел содержит от ${\textstyle t-1}$ ${\textstyle t-1}$ до ${\textstyle 2t-1}$ ${\textstyle 2t-1}$ ключей; листья не являются исключением из этого правила. Здесь ${\textstyle t}$ ${\textstyle t}$ — параметр дерева, не меньший 2 (и обычно принимающий значения от 50 до 2000 в зависимости от размера ключа относительно размера страницы, в свою очередь определяемого размером содержательной записи).
У листьев нет потомков; для всех других узлов, содержащих ключи K 1 , … , K n , {\displaystyle K_{1},\dots ,K_{n},} заданный узел содержит ( n + 1 ) {\displaystyle (n+1)} потомков. При этом:
- первый потомок и все его потомки содержат ключи из интервала $(-\infty ,K_{1});$ $(-\infty ,K_{1});$
- для $2\leqslant i\leqslant n$ $2 \leqslant i \leqslant n$ $i$ $i$ -й потомок и все его потомки содержат ключи из интервала $(K_{i-1},K_{i});$ $(K_{i-1},K_{i});$
- $(n+1)$ $(n+1)$ -й потомок и все его потомки содержат ключи из интервала $(K_{n},\infty).$ $(K_{n},\infty).$
Глубина всех листьев одинакова.
Листья имеют ссылку на соседа, позволяющую быстро обходить дерево в порядке возрастания ключей, и ссылки на данные.

Построение

Построение B⁺-дерева может требовать перестройки промежуточной структуры, это связано с тем, что количество ключей в каждом узле (кроме корня) должно быть от $t$ $t$ до $2t,$ $2t,$ где $t$ $t$ — степень (или порядок) дерева. При попытке вставить в узел ( $2t+1$ $2t+1$ )-й ключ возникает необходимость разделить этот узел, в качестве ключа-разделителя сформированных ветвей выступает ( ${\textstyle t+1}$ ${\textstyle t+1}$ )-й ключ, который помещается на соседний ярус дерева. Особым же случаем является разделение корня, так как в этом случае увеличивается число ярусов дерева. Особенностью разделения листа B⁺-дерева является то, что он делится на неравные части. При разделении внутреннего узла или корня возникают узлы с равным числом ключей $k.$ $k.$ Разделение листа может вызвать «цепную реакцию» деления узлов, заканчивающуюся в корне.

Свойства структуры

В B⁺-дереве легко реализуется независимость программы от структуры информационной записи.
Поиск обязательно заканчивается в листе.
Удаление ключа имеет преимущество — удаление всегда происходит из листа.
Другие операции выполняются аналогично B-деревьям.
B⁺-деревья требуют больше памяти для представления, чем классические B-деревья.
B⁺-деревья имеют возможность последовательного доступа к ключам.

Основные операции над структурой

Поиск

Корень B⁺-дерева является отправной точкой для всего спектра значений, в котором каждый внутренний узел представляет собой подынтервал.

Например, пусть необходимо найти значение ключа $k$ $k$ в B⁺-дереве. Для этого ищется листовой узел, содержащий значение $k.$ $k.$ В каждом внутреннем узле нужно выяснить, на какой последующий дочерний узел необходимо следовать, внутренний узел B⁺-дерева имеет не более $t$ $t$ потомков, где каждый из них представляет собой отдельный подынтервал. Выбирается соответствующий узел с помощью поиска в ключевых значениях узла:

Function: search (k) return tree_search (k, root); Function: tree_search (k, node) if node is a leaf then return node; switch k do case k < k[0] return tree_search(k, p[0]); case k[i] ≤ k < k[i + 1] return tree_search(k, p[i + 1]); case k[d] ≤ k return tree_search(k, p[d + 1]);

(Данный псевдокод рассчитан на то, что дубликаты игнорируются.)

Добавление

Для добавления нового ключа или новой записи в первую очередь необходимо найти узел, в который их необходимо добавить. В этом случае алгоритм таков:

Если узел полностью не заполнен (количество элементов после вставки не более чем $2t-1,$ $2t-1,$ ) то добавить ключ (запись).
В противном случае необходимо расщепить узел:
- создать новый узел, затем переместить половину элементов из текущего в новый;
- добавить наименьший ключ из нового узла и адрес на него (узел) в родительский;
- если родительский узел заполнен, аналогично разделить его:
  - добавить средний ключ в родительский узел;
- повторять, пока родительский узел не будет нуждаться в расщеплении.
Если расщепляется корень — создать новый корень, имеющий один ключ и два указателя (ключ, который добавляется к корню, удаляется из своего узла)

B-деревья, в отличие от B⁺-деревьев, расширяются со стороны корня, а не листьев.

Удаление

Для удаления ключа или записи в первую очередь необходимо найти листовой узел, в котором они находятся. Алгоритм удаления от листового узла:

Если узел хотя бы наполовину заполнен — завершение алгоритма;
Если узел имеет меньше элементов, то:
- выполнить попытку перераспределения элементов, то есть добавить в узел элемент из «брата» — элемента с общим предком.
- если выполнить перераспределение не удалось, объединить узел с «братом».
Если произошло объединение, удалить ключ или запись, которые указывают на удалённый узел или его «брата» из родительского узла.

Объединение может распространяться на корень, тогда происходит уменьшение высоты дерева.

Вычислительная сложность операций

Вычислительная сложность каждой операции в худшем случае: $O(\log {\frac {t}{2n}}),$ $O(\log {\frac {t}{2n}}),$ где $t$ $t$ — порядок дерева или коэффициент ветвления; $n$ $n$ — количество ~~элементов в дереве~~ ветвей в узлах дерева.

Примечания

Douglas Comer. (англ.) // ACM Computing Surveys. — 1979. — June (vol. 11 , no. 2). — P. 121—137 . — ISSN . 17 ноября 2015 года.

Литература

Зубов В. С., Шевченко И. В. Глава 6. Поиск в недвоичных деревьях - B-деревьях // Структуры и методы обработки данных. Практикум в среде Delphi. — Филинъ, 2004. — С. 144—164. — ISBN 5-9216-0053-9 .
Дональд Кнут . 4. Генерация всех деревьев. История комбинаторной генерации // Искусство программирования = The Art of Computer Programming. — М. : , 2007. — Т. 4. — С. 160. — ISBN 0-321-33570-8 .