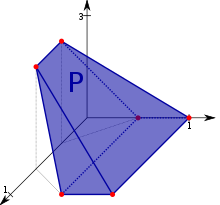
Однородный многогранник — многогранник , грани которого являются правильными многоугольниками , и он вершинно транзитивен ( транзитивен относительно вершин , а также изогонален, то есть имеется движение , переводящее вершину в любую другую). Отсюда следует, что все вершины конгруэнтны , и многогранник имеет высокую степень зеркальной и вращательной симметрии .

Однородные многогранники можно разделить на выпуклые формы с гранями в виде выпуклых правильных многоугольников и звёздчатые формы. Звёздчатые формы имеют грани в виде правильных звёздчатых многоугольников , вершинных фигур или обоих видов вместе.

Список включает:

• все 75 непризматических однородных многогранников;
• некоторых представителей бесконечного множества призм и антипризм ;
• один специальный случай, многогранник Скиллинга с пересекающимися рёбрами.

В 1970-м году советским ученым Соповым доказано , что существует только 75 однородных многогранников, не входящих в бесконечные серии призм и антипризм . Джон Скиллинг (John Skilling) открыл ещё один многогранник, ослабив условие, что ребро может принадлежать только двум граням. Некоторые авторы не считают этот многогранник однородным, поскольку некоторые пары рёбер совпадают.

Не включены:

• 40 потенциальных однородных многогранников с вырожденными вершинными фигурами , имеющих пересекающиеся рёбра (не перечислены Коксетером );
• Однородные мозаики (бесконечные многогранники)
  • 11 евклидовых
  • 14 евклидовых
  • Бесконечное число однородных мозаик на гиперболической плоскости .

Нумерация

Используются четыре схемы нумерации однородных многогранников, различающихся буквами:

• [ C ] Коксетер с соавторами (1954) . Список содержит выпуклые виды с номерами от 15 до 32, три призматических вида (номера 33—35) и невыпуклые виды (номера 36—92).
• [ W ] Веннинджер (1974) . Список содержит 119 фигур: номера 1—5 для платоновых тел, 6—18 для архимедовых тел, 19—66 для звёздчатых видов, включая 4 правильных невыпуклых многогранника и 67—119 для невыпуклых однородных многогранников.
• [ K ] Kaleido (программа , 1993). Список содержит 80 фигур, номера сгруппированы по симметрии: 1—5 представляют бесконечные серии призматических форм с , 6—9 с тетраэдральной симметрией , 10—26 с , 46—80 с икосаэдральной симметрией .
• [ U ] Mathematica (программа, 1993) . В программе, в общем, используется та же нумерации, что и в программе Kaleido, только первые 5 призматических вида перенесены в конец списка, так что непризматические виды получили номера 1—75.

Список многогранников

Выпуклые формы перечислены в порядке степени вершинных конфигураций от 3 граней/вершин и далее, и по увеличению сторон у грани. Это упорядочение позволяет показать топологическую схожесть.

Выпуклые однородные многогранники

Название	Рисунок	Тип вершинной конфигурации	Символ Витхоффа	Симм.	C#	W#	U#	K#	Вер- шин	Рё- бер	Гра- ней	${\displaystyle \chi }$	Плот- ность	Граней по типам
Тетраэдр		3.3.3	3 | 2 3	T d	C15	W001	U01	K06	4	6	4	2	1	4{3}
Треугольная призма		3.4.4	2 3 | 2	D 3h	C33a	--	U76a	K01a	6	9	5	2	1	2{3} +3{4}
Усечённый тетраэдр		3.6.6	2 3 | 3	T d	C16	W006	U02	K07	12	18	8	2	1	4{3} +4{6}
Усечённый куб		3.8.8	2 3 | 4	O h	C21	W008	U09	K14	24	36	14	2	1	8{3} +6{8}
Усечённый додекаэдр		3.10.10	2 3 | 5	I h	C29	W010	U26	K31	60	90	32	2	1	20{3} +12{10}
Куб		4.4.4	3 | 2 4	O h	C18	W003	U06	K11	8	12	6	2	1	6{4}
Пятиугольная призма		4.4.5	2 5 | 2	D 5h	C33b	--	U76b	K01b	10	15	7	2	1	5{4} +2{5}
Шестиугольная призма		4.4.6	2 6 | 2	D 6h	C33c	--	U76c	K01c	12	18	8	2	1	6{4} +2{6}
Восьмиугольная призма		4.4.8	2 8 | 2	D 8h	C33e	--	U76e	K01e	16	24	10	2	1	8{4} +2{8}
Десятиугольная призма		4.4.10	2 10 | 2	D 10h	C33g	--	U76g	K01g	20	30	12	2	1	10{4} +2{10}
		4.4.12	2 12 | 2	D 12h	C33i	--	U76i	K01i	24	36	14	2	1	12{4} +2{12}
Усечённый октаэдр		4.6.6	2 4 | 3	O h	C20	W007	U08	K13	24	36	14	2	1	6{4} +8{6}
Усечённый кубооктаэдр		4.6.8	2 3 4 |	O h	C23	W015	U11	K16	48	72	26	2	1	12{4} +8{6} +6{8}
Ромбоусечённый икосододекаэдр		4.6.10	2 3 5 |	I h	C31	W016	U28	K33	120	180	62	2	1	30{4} +20{6} +12{10}
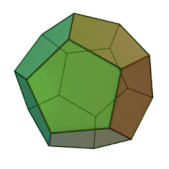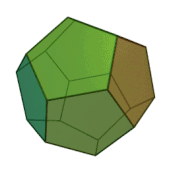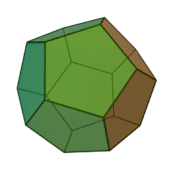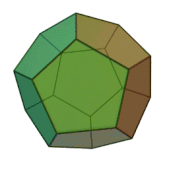
Додекаэдр		5.5.5	3 | 2 5	I h	C26	W005	U23	K28	20	30	12	2	1	12{5}
Усечённый икосаэдр		5.6.6	2 5 | 3	I h	C27	W009	U25	K30	60	90	32	2	1	12{5} +20{6}
Октаэдр		3.3.3.3	4 | 2 3	O h	C17	W002	U05	K10	6	12	8	2	1	8{3}
Квадратная антипризма		3.3.3.4	| 2 2 4	D 4d	C34a	--	U77a	K02a	8	16	10	2	1	8{3} +2{4}
Пятиугольная антипризма		3.3.3.5	| 2 2 5	D 5d	C34b	--	U77b	K02b	10	20	12	2	1	10{3} +2{5}
Шестиугольная антипризма		3.3.3.6	| 2 2 6	D 6d	C34c	--	U77c	K02c	12	24	14	2	1	12{3} +2{6}
		3.3.3.8	| 2 2 8	D 8d	C34e	--	U77e	K02e	16	32	18	2	1	16{3} +2{8}
		3.3.3.10	| 2 2 10	D 10d	C34g	--	U77g	K02g	20	40	22	2	1	20{3} +2{10}
		3.3.3.12	| 2 2 12	D 12d	C34i	--	U77i	K02i	24	48	26	2	1	24{3} +2{12}
Кубооктаэдр		3.4.3.4	2 | 3 4	O h	C19	W011	U07	K12	12	24	14	2	1	8{3} +6{4}
Ромбокубооктаэдр		3.4.4.4	3 4 | 2	O h	C22	W013	U10	K15	24	48	26	2	1	8{3} +(6+12){4}
Ромбоикосододекаэдр		3.4.5.4	3 5 | 2	I h	C30	W014	U27	K32	60	120	62	2	1	20{3} +30{4} +12{5}
Икосододекаэдр		3.5.3.5	2 | 3 5	I h	C28	W012	U24	K29	30	60	32	2	1	20{3} +12{5}
Икосаэдр		3.3.3.3.3	5 | 2 3	I h	C25	W004	U22	K27	12	30	20	2	1	20{3}
Плосконосый куб		3.3.3.3.4	| 2 3 4	O	C24	W017	U12	K17	24	60	38	2	1	(8+24){3} +6{4}
Плосконосый додекаэдр		3.3.3.3.5	| 2 3 5	I	C32	W018	U29	K34	60	150	92	2	1	(20+60){3} +12{5}

Однородные звёздчатые многогранники

Название	Рисунок	Символ Витхоффа	Тип вершинной конфигурации	Симм.	C#	W#	U#	K#	Вер- шин	Рё- бер	Гра- ней	${\displaystyle \chi }$	Плот- ность	Граней по типам
		3 / 2 3 | 3	6. 3 / 2 .6.3	O h	C37	W068	U03	K08	12	24	12	0		8{3}+4{6}
Тетрагемигексаэдр		3 / 2 3 | 2	4. 3 / 2 .4.3	T d	C36	W067	U04	K09	6	12	7	1		4{3}+3{4}
		4 / 3 4 | 3	6. 4 / 3 .6.4	O h	C51	W078	U15	K20	12	24	10	-2		6{4}+4{6}
Большой додекаэдр		5 / 2 | 2 5	(5.5.5.5.5)/ 2	I h	C44	W021	U35	K40	12	30	12	-6	3	12{5}
Большой икосаэдр		5 / 2 | 2 3	(3.3.3.3.3)/ 2	I h	C69	W041	U53	K58	12	30	20	2	7	20{3}
		3 / 2 | 3 5	(5.3.5.3.5.3)/ 2	I h	C61	W087	U47	K52	20	60	32	-8	6	20{3}+12{5}
		2 4 ( 3 / 2 4 / 2 ) |	4.8. 4 / 3 .8	O h	C60	W086	U18	K23	24	48	18	-6		12{4}+6{8}
		3 / 2 4 | 4	8. 3 / 2 .8.4	O h	C38	W069	U13	K18	24	48	20	-4	2	8{3}+6{4}+6{8}
		3 / 2 4 | 2	4. 3 / 2 .4.4	O h	C59	W085	U17	K22	24	48	26	2	5	8{3}+(6+12){4}
		5 / 4 5 | 5	10. 5 / 4 .10.5	I h	C65	W091	U51	K56	30	60	18	-12		12{5}+6{10}
		5 / 4 5 | 3	6. 5 / 4 .6.5	I h	C81	W102	U65	K70	30	60	22	-8		12{5}+10{6}
		3 / 2 3 | 5	10. 3 / 2 .10.3	I h	C63	W089	U49	K54	30	60	26	-4		20{3}+6{10}
		3 5 ( 3 / 2 5 / 4 ) |	10.6. 10 / 9 . 6 / 5	I h	C64	W090	U50	K55	60	120	32	-28		20{6}+12{10}
		2 5 ( 3 / 2 5 / 2 ) |	10.4. 10 / 9 . 4 / 3	I h	C46	W074	U39	K44	60	120	42	-18		30{4}+12{10}
		3 / 2 5 | 5	10. 3 / 2 .10.5	I h	C42	W072	U33	K38	60	120	44	-16	2	20{3}+12{5}+12{10}
		2 3 ( 5 / 4 5 / 2 ) |	6.4. 6 / 5 . 4 / 3	I h	C72	W096	U56	K61	60	120	50	-10		30{4}+20{6}
		3 / 2 5 | 3	6. 3 / 2 .6.5	I h	C62	W088	U48	K53	60	120	52	-8	6	20{3}+12{5}+20{6}
Пентаграммная призма		2 5 / 2 | 2	5 / 2 .4.4	D 5h	C33b	--	U78a	K03a	10	15	7	2	2	5{4}+2{ 5 / 2 }
		2 7 / 2 | 2	7 / 2 .4.4	D 7h	C33d	--	U78b	K03b	14	21	9	2	2	7{4}+2{ 7 / 2 }
		2 7 / 3 | 2	7 / 3 .4.4	D 7h	C33d	--	U78c	K03c	14	21	9	2	3	7{4}+2{ 7 / 3 }
		2 8 / 3 | 2	8 / 3 .4.4	D 8h	C33e	--	U78d	K03d	16	24	10	2	3	8{4}+2{ 8 / 3 }
		| 2 2 5 / 2	5 / 2 .3.3.3	D 5h	C34b	--	U79a	K04a	10	20	12	2	2	10{3}+2{ 5 / 2 }
		| 2 2 5 / 3	5 / 3 .3.3.3	D 5d	C35a	--	U80a	K05a	10	20	12	2	3	10{3}+2{ 5 / 2 }
		| 2 2 7 / 2	7 / 2 .3.3.3	D 7h	C34d	--	U79b	K04b	14	28	16	2	3	14{3}+2{ 7 / 2 }
		| 2 2 7 / 3	7 / 3 .3.3.3	D 7d	C34d	--	U79c	K04c	14	28	16	2	3	14{3}+2{ 7 / 3 }
		| 2 2 7 / 4	7 / 4 .3.3.3	D 7h	C35b	--	U80b	K05b	14	28	16	2	4	14{3}+2{ 7 / 3 }
		| 2 2 8 / 3	8 / 3 .3.3.3	D 8d	C34e	--	U79d	K04d	16	32	18	2	3	16{3}+2{ 8 / 3 }
		| 2 2 8 / 5	8 / 5 .3.3.3	D 8d	C35c	--	U80c	K05c	16	32	18	2	5	16{3}+2{ 8 / 3 }
Малый звёздчатый додекаэдр		5 | 2 5 / 2	( 5 / 2 ) 5	I h	C43	W020	U34	K39	12	30	12	-6	3	12{ 5 / 2 }
Большой звёздчатый додекаэдр		3 | 2 5 / 2	( 5 / 2 ) 3	I h	C68	W022	U52	K57	20	30	12	2	7	12{ 5 / 2 }
		3 | 5 / 3 5	( 5 / 3 .5) 3	I h	C53	W080	U41	K46	20	60	24	-16	4	12{5}+12{ 5 / 2 }
		3 | 5 / 2 3	( 5 / 2 .3) 3	I h	C39	W070	U30	K35	20	60	32	-8	2	20{3}+12{ 5 / 2 }
		2 3 | 4 / 3	8 / 3 . 8 / 3 .3	O h	C66	W092	U19	K24	24	36	14	2	7	8{3}+6{ 8 / 3 }
Большой ромбогексаэдр		2 4 / 3 ( 3 / 2 4 / 2 ) |	4. 8 / 3 . 4 / 3 . 8 / 5	O h	C82	W103	U21	K26	24	48	18	-6		12{4}+6{ 8 / 3 }
		3 4 | 4 / 3	8 / 3 .3. 8 / 3 .4	O h	C50	W077	U14	K19	24	48	20	-4	4	8{3}+6{4}+6{ 8 / 3 }
		5 / 3 5 / 2 | 5 / 3	10 / 3 . 5 / 3 . 10 / 3 . 5 / 2	I h	C86	W107	U70	K75	30	60	18	-12		12{ 5 / 2 }+6{ 10 / 3 }
		5 / 3 5 / 2 | 3	6. 5 / 3 .6. 5 / 2	I h	C78	W100	U62	K67	30	60	22	-8		12{ 5 / 2 }+10{6}
Додекододекаэдр		2 | 5 / 2 5	( 5 / 2 .5) 2	I h	C45	W073	U36	K41	30	60	24	-6	3	12{5}+12{ 5 / 2 }
		3 / 2 3 | 5 / 3	10 / 3 . 3 / 2 . 10 / 3 .3	I h	C85	W106	U71	K76	30	60	26	-4		20{3}+6{ 10 / 3 }
Большой икосо- додекаэдр		2 | 5 / 2 3	( 5 / 2 .3) 2	I h	C70	W094	U54	K59	30	60	32	2	7	20{3}+12{ 5 / 2 }
		4 / 3 3 4 |	8 / 3 .6.8	O h	C52	W079	U16	K21	48	72	20	-4	4	8{6}+6{8}+6{ 8 / 3 }
		4 / 3 2 3 |	8 / 3 .4. 6 / 5	O h	C67	W093	U20	K25	48	72	26	2	1	12{4}+8{6}+6{ 8 / 3 }
		2 5 / 2 | 5	10.10. 5 / 2	I h	C47	W075	U37	K42	60	90	24	-6	3	12{ 5 / 2 }+12{10}
		2 5 | 5 / 3	10 / 3 . 10 / 3 .5	I h	C74	W097	U58	K63	60	90	24	-6	9	12{5}+12{ 10 / 3 }
		2 3 | 5 / 3	10 / 3 . 10 / 3 .3	I h	C83	W104	U66	K71	60	90	32	2	13	20{3}+12{ 10 / 3 }
		2 5 / 2 | 3	6.6. 5 / 2	I h	C71	W095	U55	K60	60	90	32	2	7	12{ 5 / 2 }+20{6}
		3 5 / 3 ( 3 / 2 5 / 2 ) |	6. 10 / 3 . 6 / 5 . 10 / 7	I h	C79	W101	U63	K68	60	120	32	-28		20{6}+12{ 10 / 3 }
		2 5 / 3 ( 3 / 2 5 / 4 ) |	4. 10 / 3 . 4 / 3 . 10 / 7	I h	C89	W109	U73	K78	60	120	42	-18		30{4}+12{ 10 / 3 }
		5 / 3 5 | 3	6. 5 / 3 .6.5	I h	C56	W083	U44	K49	60	120	44	-16	4	12{5}+12{ 5 / 2 }+20{6}
		5 / 3 3 | 5	10. 5 / 3 .10.3	I h	C55	W082	U43	K48	60	120	44	-16	4	20{3}+12{ ;5 / 2 }+12{10}
		3 5 | 5 / 3	10 / 3 .3. 10 / 3 .5	I h	C54	W081	U42	K47	60	120	44	-16	4	20{3}+12{5}+12{ 10 / 3 }
		5 / 2 3 | 5 / 3	10 / 3 . 5 / 2 . 10 / 3 .3	I h	C77	W099	U61	K66	60	120	44	-16	10	20{3}+12{ 5 / 2 }+12{ 10 / 3 }
		5 / 2 3 | 3	6. 5 / 2 .6.3	I h	C40	W071	U31	K36	60	120	52	-8	2	20{3}+12{ 5 / 2 }+20{6}
		5 / 2 5 | 2	4. 5 / 2 .4.5	I h	C48	W076	U38	K43	60	120	54	-6	3	30{4}+12{5}+12{ 5 / 2 }
		5 / 3 3 | 2	4. 5 / 3 .4.3	I h	C84	W105	U67	K72	60	120	62	2	13	20{3}+30{4}+12{ 5 / 2 }
		5 / 3 3 5 |	10 / 3 .6.10	I h	C57	W084	U45	K50	120	180	44	-16	4	20{6}+12{10}+12{ 10 / 3 }
		5 / 3 2 5 |	10 / 3 .4. 10 / 9	I h	C75	W098	U59	K64	120	180	54	-6	3	30{4}+12{10}+12{ 10 / 3 }
		5 / 3 2 3 |	10 / 3 .4.6	I h	C87	W108	U68	K73	120	180	62	2	13	30{4}+20{6}+12{ 10 / 3 }
		| 2 5 / 2 5	3.3. 5 / 2 .3.5	I	C49	W111	U40	K45	60	150	84	-6	3	60{3}+12{5}+12{ 5 / 2 }
		| 5 / 3 2 5	3 5 / 3 .3.3.5	I	C76	W114	U60	K65	60	150	84	-6	9	60{3}+12{5}+12{ 5 / 2 }
		| 2 5 / 2 3	3 4 . 5 / 2	I	C73	W116	U57	K62	60	150	92	2	7	(20+60){3}+12{ 5 / 2 }
		| 5 / 3 2 3	3 3 . 5 / 3	I	C88	W113	U69	K74	60	150	92	2	13	(20+60){3}+12{ 5 / 2 }
Большой вывернутый обратноплосконосый икосододекаэдр		| 3 / 2 5 / 3 2	(3 4 . 5 / 2 )/ 2	I	C90	W117	U74	K79	60	150	92	2	37	(20+60){3}+12{ 5 / 2 }
		| 5 / 3 5 / 2 3	3 3 . 5 / 3 .3. 5 / 2	I	C80	W115	U64	K69	60	180	104	-16	10	(20+60){3}+(12+12){ 5 / 2 }
		| 5 / 3 3 5	3 3 .5. 5 / 3	I	C58	W112	U46	K51	60	180	104	-16	4	(20+60){3}+12{5}+12{ 5 / 2 }
		| 5 / 2 3 3	3 5 . 5 / 2	I h	C41	W110	U32	K37	60	180	112	-8	2	(40+60){3}+12{ 5 / 2 }
		| 3 / 2 3 / 2 5 / 2	(3 5 . 5 / 3 )/ 2	I h	C91	W118	U72	K77	60	180	112	-8	38	(40+60){3}+12{ 5 / 2 }
		| 3 / 2 5 / 3 3 5 / 2	(4. 5 / 3 .4.3. 4. 5 / 2 .4. 3 / 2 )/ 2	I h	C92	W119	U75	K80	60	240	124	-56		40{3}+60{4}+24{ 5 / 2 }

Особый случай

Название по Бауэру (Bower)	Рисунок	Символ Витхоффа	Вершинная конфигурация	Группа симметрии	C#	W#	U#	K#	Вершин	Рёбер	Граней	${\displaystyle \chi }$	Плот- ность	Граней по типам
		| ( 3 / 2 ) 5 / 3 (3) 5 / 2	( 5 / 2 .4.3.3.3.4. 5 / 3 .4. 3 / 2 . 3 / 2 . 3 / 2 .4)/ 2	I h	--	--	--	--	60	240 (*)	204	24		120{3}+60{4}+24{ 5 / 2 }

(*): В Большом биплосконосом биромбобидодекаэдре 120 из 240 рёбер принадлежат четырём граням. Если эти 120 рёбер считать как две пары совпадающих рёбер, где каждое ребро принадлежит только двум граням, то всего будет 360 рёбер и эйлерова характеристика становится равной −88. Ввиду этой вырожденности рёбер многогранник не всеми признаётся как однородный.

Обозначения в колонках

• U# — Однородные номера: U01—U80 (Тетраэдр первый, Призмы с номерами 76+)
• K# — Kaleido software номера: K01—K80 (K _n = U _n-5 для n = 6 to 80) (призмы 1—5, тетраэдр и далее 6+)
• W# — Модели Магнуса Веннинджера : W001—W119
  • 1—18 — 5 выпуклых правильных и 13 выпуклых полуправильных
  • 20—22, 41 — 4 невыпуклые правильные
  • 19—66 — 48 звёздчатых форм/соединений (нерегулярные не даны в этом списке)
  • 67—109 — 43 невыпуклых остроносых однородных многогранников
  • 110—119 — 10 невыпуклых плосконосых однородных многогранников
• ${\displaystyle \chi }$ — эйлерова характеристика . Однородные мозаики на плоскости соответствуют топологии тора с эйлеровой характеристикой ноль.
• Плотность — представляет число оборотов многогранника вокруг центра. Число отсутствует для неориентируемых многогранников и для (многогранников, имеющих грани, проходящие через центр многогранника), для которых нет чёткого определения плотности.
• Замечание о рисунках вершинных фигур:
  • Светлые отрезки представляют «вершинную фигуру» многогранника. Цветные грани включены в рисунок вершинной фигуры, чтобы видеть их связи. Некоторые пересекающиеся грани нарисованы визуально неверно, поскольку визуально они не показывают, какие части находится впереди.

Примечания

Литература

• М. Веннинджер . Модели многогранников. — «Мир», 1974.
• Magnus Wenninger. Dual Models. — Cambridge University Press, 1983. — ISBN 0-521-54325-8 .
• H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller. Uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246 , вып. 916 . — С. 401—450 . — ISSN . — doi : . — JSTOR .
• H. S. M. Coxeter , , H. T. Flather, J. F. Petrie. The Fifty-nine Icosahedra. — University of Toronto studies, 1938. — (mathematical series 6: 1–26.). Third edition (1999) Tarquin ISBN 978-1-899618-32-3 .
• J. Skilling. The complete set of uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — 1975. — Т. 278 . — С. 111–135 . — ISSN . — doi : . — JSTOR .
• Roman E. Maeder. Uniform Polyhedra // The Mathematica Journal. — 1993. — Т. 3 , вып. 4 .

Ссылки

• (неопр.) . Дата обращения: 15 ноября 2015. 9 июля 2010 года. — Software able to generate and print nets for all uniform polyhedra. Used to create most images on this page.
• Robert Webb. (неопр.) . Дата обращения: 15 ноября 2015. 5 декабря 2015 года.
• от 7 ноября 2017 на Wayback Machine // , выпуск 8, 1970 год, стр. 139-156.
• Uniform indexing: U1—U80, (Tetrahedron first)
  • Paul Bourke. (неопр.) . 11 сентября 2006 года.
  • Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
  • Roman E. Maeder. (неопр.) . MathConsult AG. Дата обращения: 15 ноября 2015. 5 июня 2014 года.
    • (неопр.) . Дата обращения: 15 ноября 2015. 21 октября 2014 года.
  • Sam Gratrix. (неопр.) . Gratrix.net. Дата обращения: 15 ноября 2015. Архивировано из 10 ноября 2017 года.
  • (недоступная ссылка — )
  • James R. Buddenhagen. (неопр.) . Дата обращения: 15 ноября 2015. 4 марта 2016 года.
• Kaleido Indexing: K1-K80 (Pentagonal prism first)
  • Zvi Har’El. (неопр.) . Архивировано из 20 мая 2011 года.
    • (неопр.) . Архивировано из 15 июля 2009 года.
  • V. Bulatov. (неопр.) . Дата обращения: 15 ноября 2015. 25 июля 2011 года.
  • Jim McNeill. (неопр.) . Дата обращения: 15 ноября 2015. 24 сентября 2015 года.
  • U. Mikloweit. (неопр.) . Дата обращения: 15 ноября 2015. 24 сентября 2015 года.