Interested Article - Звезда (геометрия)

- 2020-09-02
- 1
|
|
В этой статье
слишком короткая преамбула
.
|
|
|
Эту статью необходимо
исправить в соответствии с
правилом Википедии об оформлении статей
.
|
|
|
В статье
не хватает
ссылок на источники
(см.
рекомендации по поиску
).
|
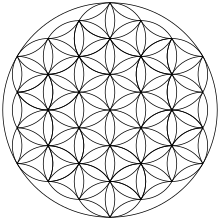
Звезда — вид плоских невыпуклых многоугольников , не имеющий однозначного математического определения.
Звёздчатый многоугольник


Звёздчатый многоугольник — многоугольник , у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника . Стороны звёздчатого многоугольника могут пересекаться между собой. Существует множество звёздчатых многоугольников или звёзд , среди них пентаграмма , гексаграмма , две гептаграммы , октаграмма , , .
Звёздчатые многоугольники можно получить, продолжая одновременно все стороны правильного многоугольника после их пересечения в его вершинах до их следующего пересечения в точках, которые и являются вершинами звёздчатого многоугольника. Полученный звёздчатый многоугольник будет звёздчатой формой правильного многоугольника, из которого он получен. Вершинами звёздчатого многоугольника будут считаться только точки, в которых сходятся стороны этого многоугольника, но не точки пересечения этих сторон; звёздчатая форма данного многоугольника имеет столько же вершин, сколько он сам. Указанную операцию невозможно проделать с правильным треугольником и квадратом, так как после продления их стороны более не пересекаются; среди правильных многоугольников звёздчатые формы имеют только многоугольники с числом сторон более четырёх. Звёздчатой формой правильного пятиугольника (пентагона) является пентаграмма .
В ином способе получить звёздчатую форму правильного n -угольника каждая его вершина соединяется с m -й от неё на окружности по часовой стрелке. Звезда, полученная таким образом, обозначается как {n/m} . При этом точки пересечения сторон между собой не рассматриваются как вершины. Такая звезда имеет n вершин и n сторон, также как и правильный n -угольник.
Соотношение радиусов 2 окружностей правильной звезды с вышеприведённым вариантом построения: внешней (на которой лежат вершины углов лучей звезды) и внутренней (на которой лежат точки пересечения сторон соседних лучей) вычисляется по формуле:
Звёзды могут быть связными (нераспадающимися едиными многоугольниками), не являясь соединениями других правильных или звёздчатых многоугольников (как в случае с пентаграммой), а могут быть несвязными , распадаясь на несколько одинаковых правильных многоугольников или связных звёзд (примером чему служит звёздчатая форма шестиугольника — гексаграмма , являющаяся соединением двух треугольников).
У правильного многоугольника может быть несколько звёздчатых форм, количество которых зависит от того, сколько раз его стороны пересекаются между собой после их продления, примером чего является семиугольник, имеющий 2 звёздчатые формы (два вида семиконечной звезды).
| Количество вершин правильного многоугольника | Количество звёздчатых форм правильного многоугольника | Количество нераспадающихся (связных) звёздных многоугольников среди звёздчатых форм | Количество вершин правильного многоугольника, расположенных между двумя вершинами звёздного многоугольника |
|---|---|---|---|
| 5 | 1 | 1 | 1 |
| 6 | 1 | 0 | |
| 7 | 2 | 2 | 2; 3 |
| 8 | 2 | 1 | 2 |
| 9 | 3 | 2 | 1; 3 |
| 10 | 3 | 1 | 2 |
| 11 | 4 | 4 | 1; 2; 3; 4 |
| 12 | 4 | 1 | 4 |

Пурпурные — выпуклые многоугольники.
Зелёные — связные звёзды {n/m} (где n и m взаимно простые числа ), см. также Фигуры Лиссажу .
Чёрные — не связные звёзды {n/m} (где n и m не взаимно простые числа ).
Синие прямые соединяют многоугольник (выпуклый или связную звезду) со всеми не связными звёздами, являющимися соединениями (после поворота) разного количества одинаковых многоугольников, таких же как этот
Вершинно-транзитивный многоугольник

|
|
Этот раздел статьи
ещё
не написан
.
|
См. также
- Звёздчатый многогранник
- Звёздная область
- Пифагорейский пентакл
- Пентаграмма
- Октаграмма
- Ромб
- Эннеаграмма (геометрия)
- Правильный семиугольник
- Моравская звезда
Ссылки
- М. Веннинджер . . — Москва: Мир, 1974. (рус.)
- 2020-09-02
- 1