Interested Article - Антипризма

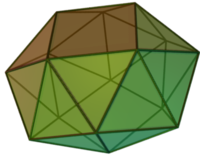
Антипризма — полуправильный многогранник , у которого две параллельные грани (основания) — равные между собой правильные n -угольники , а остальные 2 n граней (боковые грани) — правильные треугольники.
Октаэдр является антипризмой с треугольными основаниями. Икосаэдр сложен из пятиугольной антипризмы и двух правильных пятиугольных пирамид .
Объем и площадь поверхности
Пусть
 — длина ребра правильной антипризмы. Тогда её объем вычисляется по формуле:
— длина ребра правильной антипризмы. Тогда её объем вычисляется по формуле:
а площадь поверхности по формуле:
Вариации и обобщения

-
Скрученная квадратная антипризма получается из антипризмы поворотом одного из оснований при сохранении комбинаторной структуры граней рёбер и вершин.
- Многогранник Шёнхардта — скрученная треугольная антипризма.
| Многогранник |
|
|
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика |
|
|
|
|
|
|
|
|
||||
| Конфигурация | V2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | ... |
| * n 62 варианты симметрии правильных мозаик: {6, n } | ||||||||
|---|---|---|---|---|---|---|---|---|
| Сферические | Евклидовы | Гиперболические мозаики | ||||||

{6,2} |

{6,3} |

|

|

|

|

|
... |

|
См. также
|
|
В статье
не хватает
ссылок на источники
(см.
рекомендации по поиску
).
Информация должна быть
проверяема
, иначе она может быть удалена. Вы можете
статью, добавив ссылки на
авторитетные источники
в виде
сносок
.
(
24 июня 2022
)
|
|
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Периодичные | |||||||||
| Апериодичные | |||||||||
| Другие | |||||||||
|
По
вершинной
конфигурации |
|
||||||||
Источник —
- Tags: