Interested Article - Правильный многоугольник

- 2021-10-27
- 1
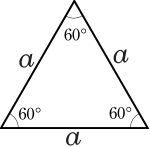
Пра́вильный многоуго́льник — выпуклый многоугольник , у которого равны все стороны и все углы между смежными сторонами.
Определение правильного многоугольника может зависеть от определения многоугольника : если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.
Связанные определения
- Центром правильного многоугольника называется его центр масс , совпадающий с центрами его вписанной и описанной окружностей.
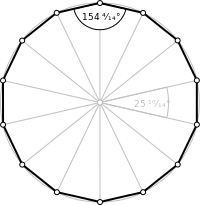
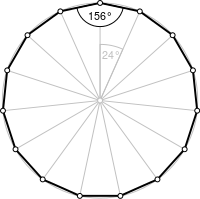
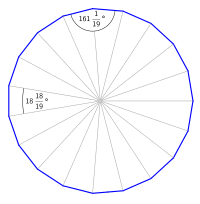
- Центральным углом правильного многоугольника называется центральный угол его описанной окружности , опирающийся на его сторону. Величина центрального угла правильного -угольника равна .
Свойства
Координаты
Пусть и — координаты центра, а — радиус описанной вокруг правильного многоугольника окружности , — угловая координата первой вершины относительно центра, тогда декартовы координаты вершин правильного n-угольника определяются формулами:
где принимает значения от до .
Размеры

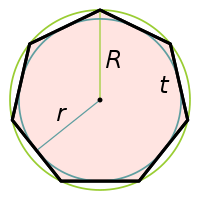
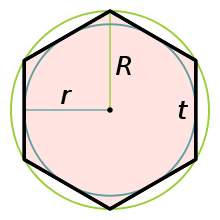
Пусть — радиус описанной вокруг правильного многоугольника окружности , тогда радиус вписанной окружности равен
- ,
а длина стороны многоугольника равна
Площадь
Площадь правильного многоугольника с числом сторон и длиной стороны составляет:
- .
Площадь правильного многоугольника с числом сторон , вписанного в окружность радиуса , составляет:
- .
Площадь правильного многоугольника с числом сторон , описанного вокруг окружности радиуса , составляет:
Площадь правильного многоугольника с числом сторон равна
- ,
где — радиус вписанной окружности многоугольника, — длина его стороны, а - его периметр.
Периметр
Если нужно вычислить длину стороны правильного n-угольника, вписанного в окружность, зная длину окружности можно вычислить длину одной стороны многоугольника:
- — длина стороны правильного n-угольника.
Периметр равен
где — число сторон многоугольника.
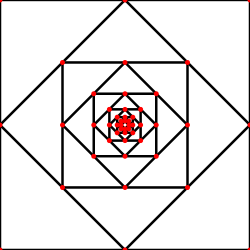
Свойства диагоналей правильных многоугольников
- Максимальное количество диагоналей правильного -угольника, пересекающихся в одной точке, не являющейся его вершиной или центром, равно:
- Существуют лишь три исключения: данное число равно в треугольнике , в шестиугольнике и в двенадцатиугольнике .
- При чётном в центре многоугольника пересекается диагонали.
Введём функцию , равную в случае, если делится на , и равную в противном случае. Тогда:
- Количество точек пересечения диагоналей правильного -угольника равно
- Где - число сочетаний из по .
- Количество частей, на которые правильный -угольник делят его диагонали, равно
- .
Применение
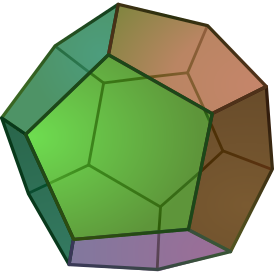
Правильными многоугольниками по определению являются грани правильных многогранников .
Древнегреческие математики ( Антифонт , Брисон Гераклейский , Архимед и др.) использовали правильные многоугольники для вычисления числа π . Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круг а.
История
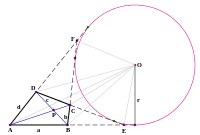
Построение циркулем и линейкой правильного многоугольника с сторонами оставалось проблемой для математиков вплоть до XIX века . Такое построение идентично разделению окружности на равных частей, так как, соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник.
Евклид в своих « Началах » занимался построением правильных многоугольников в книге IV, решая задачу для . Кроме этого, он уже определил первый критерий построимости многоугольников: хотя этот критерий и не был озвучен в «Началах», древнегреческие математики умели построить многоугольник с сторонами (при целом ), имея уже построенный многоугольник с числом сторон : пользуясь умением разбиения дуги на две части, из двух полуокружностей мы строим квадрат , потом правильный восьмиугольник , и так далее. Кроме этого, в той же книге Евклид указывает и второй критерий построимости: если известно, как строить многоугольники с и сторонами, и и взаимно простые , то можно построить и многоугольник с сторонами. Это достигается построением многоугольника с сторонами и многоугольника с сторонами так, чтобы они были вписаны в одну окружность и чтобы одна вершина у них была общей - в таком случае некоторые две вершины этих многоугольников будут являться соседними вершинами -угольника. Синтезируя эти два способа, можно прийти к выводу, что древние математики умели строить правильные многоугольники с , и сторонами при любом целом неотрицательном .
Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма , то его можно построить при помощи циркуля и линейки. На сегодняшний день известны следующие простые числа Ферма: . Вопрос о наличии или отсутствии других таких чисел остаётся открытым. Гаусс, в частности, первым смог доказать возможность построения правильного -угольника, а под конец жизни завещал выбить его на своём надгробии, однако скульптор отказался выполнять столь сложную работу .
Из результата Гаусса мгновенно следовало, что правильный многоугольник возможно построить, если число его сторон равно , где — целое неотрицательное число, а — попарно различные простые числа Ферма. Гаусс подозревал, что это условие является не только достаточным, но и необходимым, но впервые это было доказано Пьером-Лораном Ванцелем в 1836 году . Итоговая теорема, совмещающая оба результата, называется Теоремой Гаусса-Ванцеля .
Последними результатами в области построения правильных многоугольников являются явные построения 17- , 257- и 65537-угольника . Первое было найдено в 1825 году , второе — в 1832 году , а последнее — Иоганном Густавом Гермесом в 1894 году .
См. также
Примечания
- . Дата обращения: 12 мая 2020. 2 июля 2020 года.
- ↑ . Дата обращения: 16 июля 2020. 17 июля 2020 года.
- А. В. Жуков. О числе π. — М.: МЦНМО, 2002. ISBN 5-94057-030-5 .
- 2021-10-27
- 1