Interested Article - Описанный четырёхугольник

- 2020-09-29
- 1

В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник , стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников .
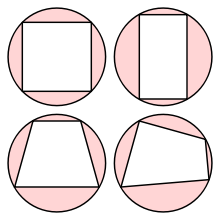
Все треугольники имеют вписанные окружности, но не все четырёхугольники. Примером четырёхугольника, в который нельзя вписать окружность, может служить прямоугольник , не являющийся квадратом. Раздел «Свойства» ниже даёт необходимые и достаточные условия, чтобы четырёхугольник был описанным.
Специальные случаи
Примерами описанных четырёхугольников могут служить дельтоиды , которые включают ромбы , которые, в свою очередь, включают квадраты . Дельтоиды — это в точности те описанные четырёхугольники, которые также являются ортодиагональными . Если четырёхугольник является описанным и вписанным четырёхугольником , он называется .
Свойства

В описанном четырёхугольнике четыре биссектрисы пересекаются в центре окружности. И наоборот, выпуклый четырёхугольник, в котором четыре биссектрисы пересекаются в одной точке, должен быть описанным, и точка пересечения биссектрис является центром вписанной окружности .
Согласно теореме Пито две пары противоположных сторон в описанном четырёхугольнике в сумме дают одно и то же число, которое равно полупериметру s четырёхугольника:
Обратно — четырёхугольник, в котором a + c = b + d , должен быть описанным.
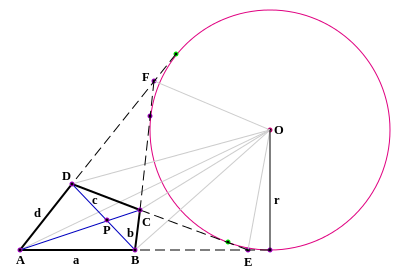
Если противоположные стороны в выпуклом четырёхугольнике ABCD (не являющемся трапецией ) пересекаются в точках E и F , то они являются касательными к окружности тогда и только тогда, когда
или
Второе равенство почти то же, что и равенство в . Разница только в знаках — в теореме Уркхарта суммы, а здесь разности (см. рисунок справа).
Другое необходимое и достаточное условие — выпуклый четырёхугольник ABCD является описанным в том и только в том случае, когда вписанные в треугольники ABC и ADC окружности касаются друг друга .
Описание по углам, образованным диагональю BD со сторонами четырёхугольника ABCD , принадлежит Иосифеску (Iosifescu). Он в 1954 доказал, что выпуклый четырёхугольник имеет вписанную окружность тогда и только тогда, когда
Далее выпуклый четырёхугольник со сторонами a , b , c , d является описанным тогда и только тогда, когда
- ,
где R a , R b , R c , R d являются радиусами окружностей, внешне касательным сторонам a , b , c , d соответственно и продолжениям смежных сторон с каждой стороны .
Некоторые другие описания известны для четырёх треугольников, образованных диагоналями.
Специальные отрезки
Восемь отрезков касательных описанного четырёхугольника являются отрезками между вершинами и точками касания на сторонах. В каждой вершине имеется два равных касательных отрезка.
Точки касания образуют вписанный четырёхугольник.
Площадь
Нетригонометрические формулы
Площадь K касательного четырёхугольника задаётся формулой
- ,
где p — полупериметр и r — радиус вписанной окружности . Ещё одна формула
- ,
дающая площадь в терминах диагоналей p , q и сторон a , b , c , d касательного четырёхугольника.
Площадь можно представить также в терминах касательных отрезков (см. выше). Если их обозначить через e , f , g , h , то касательный четырёхугольник имеет площадь
Более того, площадь касательного четырёхугольника можно выразить в терминах сторон a, b, c, d и соответствующих длин касательных отрезков e, f, g, h
Поскольку eg = fh в том и только в том случае, когда он также является вписанным, получаем, что максимальная площадь может достигаться только на четырёхугольниках, которые являются и описанными, и вписанными одновременно.
Тригонометрические формулы
Тригонометрическая формула для площади в терминах сторон a , b , c , d и двух противоположных сторон
Для заданного произведения сторон площадь будет максимальной, когда четырёхугольник является также вписанным . В этом случае , поскольку противоположные углы являются дополнительными . Это можно доказать и другим способом, используя математический анализ .
Ещё одна формула площади описанного четырёхугольника ABCD , использующая два противоположных угла
- ,
где O является центром вписанной окружности.
Фактически площадь можно выразить в терминах лишь двух смежных сторон и двух противоположных углов
Есть ещё одна формула
где θ угол (любой) между диагоналями. Формула неприменима к случаю дельтоидов, поскольку в этом случае θ равен 90° и тангенс не определён.
Неравенства
Как упомянуто было вскользь выше, площадь касательного многоугольника со сторонами a , b , c , d удовлетворяет неравенству
и равенство достигается тогда и только тогда, когда четырёхугольник является .
Согласно Т. А. Ивановой (1976), полупериметр p описанного четырёхугольника удовлетворяет неравенству
- ,
где r — радиус вписанной окружности. Неравенство превращается в равенство тогда и только тогда, когда четырёхугольник является квадратом . Это означает, что для площади S = pr, выполняется неравенство
с переходом в равенство в том и только в том случае, когда четырёхугольник — квадрат.
Свойства частей четырёхугольника

Четыре отрезка прямых между центром вписанной окружности и точками касания делят четырёхугольник на четыре прямоугольных дельтоида .
Если прямая делит описанный четырёхугольник на два многоугольника с равными площадями и равными периметрами , то эта линия проходит через инцентр .
Радиус вписанной окружности
Радиус вписанной окружности описанного четырёхугольника со сторонами a , b , c , d задаётся формулой
- ,
где S — площадь четырёхугольника, а p — полупериметр. Для описанных четырёхугольников с заданным полупериметром радиус вписанной окружности максимален, когда четырёхугольник является одновременно и вписанным .
В терминах отрезков касательных радиус вписанной окружности .
Радиус вписанной окружности можно выразить также в терминах расстояния от инцентра O до вершин описанного четырёхугольника ABCD . Если u = AO , v = BO , x = CO и y = DO , то
- ,
где .
Формулы для углов
Если e , f , g и h отрезки касательных от вершин A , B , C и D соответственно к точкам касания окружности четырёхугольником ABCD , то углы четырёхугольника можно вычислить по формулам
Угол между хордами KM и LN задаётся формулой (см. рисунок)
Диагонали
Если e , f , g и h являются отрезками касательных от A , B , C и D до точек касания вписанной окружности четырёхугольником ABCD , то длины диагоналей p = AC и q = BD равны
Хорды точек касания
Если e , f , g и h являются отрезками от вершин до точек касания, то длины хорд до противоположных точек касания равны
где хорда k соединяет стороны с длинами a = e + f и c = g + h , а хорда l соединяет стороны длиной b = f + g и d = h + e . Квадрат отношения хорд удовлетворяет соотношению
Две хорды
- перпендикулярны тогда и только тогда, когда четырёхугольник также и вписан .
- имеют одинаковые длины тогда и только тогда, описанный четырёхугольник является дельтоидом .
Хорда между сторонами AB и CD в описанном четырёхугольнике ABCD длиннее, чем хорда между сторонами BC и DA тогда и только тогда, когда средняя линия между сторонами AB и CD короче, чем средняя линия между сторонами BC и DA .
Если описанный четырёхугольник ABCD имеет точки касания M на AB и N на CD и хорда MN пересекает диагональ BD в точке P , то отношение отрезков касательных равно отношению отрезков диагонали BD .
Коллинеарные точки

Если M 1 и M 2 являются серединами диагоналей AC и BD соответственно в описанном четырёхугольнике ABCD с центром вписанной окружности O , а пары противоположных сторон пересекаются в точках E и F и M 3 — середина отрезка EF , тогда точки M 3 , M 1 , O , и M 2 лежат на одной прямой Прямая, соединяющая эти точки, называется прямой Ньютона четырёхугольника.
Если продолжения противоположных сторон описанного четырёхугольника пересекаются в точках E и F , а продолжения противоположных сторон четырёхугольника, образованного точками касания, пересекаются в точках T и S , то четыре точки E , F , T и S лежат на одной прямой
Если вписанная окружность касается сторон AB , BC , CD , DA в точках M , K , N и L соответственно, и если T M , T K , T N , T L являются изотомически сопряжёнными точками этих точек (то есть AТ M = BM и т.д.), то точка Нагеля определяется как пересечение прямых T N T M и T K T L . Обе эти прямые делят периметр четырёхугольника на две равные части. Однако важнее то, что точка Нагеля Q , "центроид площади" G и центр вписанной окружности O лежат на одной прямой, и при этом QG = 2 GO . Эта прямая называется прямой Нагеля описанного четырёхугольника .
В описанном четырёхугольнике ABCD с центром вписанной окружности O , в котором диагонали пересекаются в точке P , пусть H M , H K , H N , H L являются ортоцентрами треугольников AOB , BOC , COD и DOA соответственно. Тогда точки P , H M , H K , H N и H L лежат на одной прямой.
Конкурентные и перпендикулярные прямые
Две диагонали четырёхугольника и две хорды, соединяющие противоположные точки касания (противоположные вершины вписанного четырёхугольника), конкурентны (т.е. пересекаются в одной точке). Для того, чтобы показать это, можно воспользоваться частным случаем теоремы Брианшона , которая утверждает, что шестиугольник, все стороны которого касаются коническое сечение , имеет три диагонали, пересекающиеся в одной точке. Из описанного четырёхугольника легко получить шестиугольник с двумя углами по 180° путём вставки двух новых вершина противоположных точках касания. Все шесть сторон полученного шестиугольника являются касательными вписанной окружности, так что его диагонали пересекаются в одной точке. Но две диагонали шестиугольника совпадают с диагоналями четырёхугольника, а третья диагональ проходит через противоположные точки касания. Повторив те же рассуждения для двух других точек касания, получим требуемый результат.
Если вписанная окружность касается сторон AB , BC , CD и DA в точках M , K , N , L соответственно, то прямые MK , LN и AC конкурентны.
Если продолжения противоположных сторон описанного четырёхугольника пересекаются в точках E и F , а диагонали пересекаются в точке P , то прямая EF перпендикулярна продолжению OP , где O — центр вписанной окружности .
Свойства вписанной окружности
Отношения двух противоположных сторон описанного четырёхугольника можно выразить через расстояния от центра вписанной окружности O до соответствующих вершин
Произведение двух смежных сторон описанного четырёхугольника ABCD с центром вписанной окружности O удовлетворяет соотношению
Если O — центр вписанной окружности четырёхугольника ABCD , то
Центр вписанной окружности O совпадает с "центроидом вершин" четырёхугольника в том и только в том случае, когда
Если M 1 и M 2 являются серединами диагоналей AC и BD соответственно, то
где e , f , g и h — отрезки касательных в вершинах A , B , C и D соответственно. Комбинируя первое равенство с последним, получим, что "центроид вершин" описанного четырёхугольника совпадает с центром вписанной окружности тогда и только тогда, когда центр вписанной окружности лежит посередине между средними точками диагоналей.
Если четырёхзвенный механизм выполнен в виде описанного четырёхугольника, четырёхугольник остаётся описанным независимо от его деформации, при условии, что четырёхугольник остаётся выпуклым (Так, например, при деформации квадрата в ромб четырёхугольник остаётся описанным, хотя вписанная окружность будет меньшего размера). Если при деформации одна сторона зафиксирована, то при деформации четырёхугольника центр вписанной окружности движется по окружности радиуса , где a,b,c,d — стороны, а s — полупериметр.
Свойства четырёх внутренних треугольников

Для непересекающихся треугольниках APB , BPC , CPD , DPA , образованных диагоналями выпуклого четырёхугольника ABCD , где диагонали пересекаются в точке P , имеются следующие свойства.
Пусть r 1 , r 2 , r 3 и r 4 означают радиусы вписанных окружностей треугольников APB , BPC , CPD и DPA соответственно. Чао и Симеонов доказали, что четырёхугольник является описанным тогда и только тогда, когда
Это свойство было доказано пятью годами ранее Вайнштейном . В решении его задачи похожее свойство было дано Васильевым и Сендеровым. Если через h M , h K , h N и h L обозначить высоты тех же треугольников (опущенных из пересечения диагоналей P ), то четырёхугольник является описанным тогда и только тогда, когда
Ещё одно похожее свойство относится к радиусам вневписанных окружностей r M , r K , r N и r L для тех же четырёх треугольников (четыре вневписанные окружности касаются каждой из сторон четырёхугольника и продолжений диагоналей). Четырёхугольник является описанным в том и только в том случае, когда
Если R M , R K , R N и R L — радиусы описанных окружностей треугольников APB , BPC , CPD и DPA соответственно, то четырёхугольник ABCD является описанным тогда и только тогда, когда
В 1996 Вайнштейн, похоже, был первым, кто доказал ещё одно замечательное свойство описанных четырёхугольников, которое позднее появилось в нескольких журналах и сайтах . Свойство утверждает, что если выпуклый четырёхугольников разделён на четыре неперекрывающихся треугольника его диагоналями, центры вписанных окружностей этих треугольников лежат на одной окружности тогда и только тогда, когда четырёхугольник является описанным. Фактически центры вписанных окружностей образуют ортодиагональный вписанный четырёхугоольник . Здесь вписанные окружности можно заменить на вневписанные (касающиеся стороны и продолжения диагоналей четырёхугольника). Тогда выпуклый четырёхугольник является описанным тогда и только тогда, когда центры вневписанных окружностей являются вершинами вписанного четырёхугольника .
Выпуклый четырёхугольник ABCD , в котором диагонали пересекаются в точке P , является описанным тогда и только тогда, когда четыре центра вневписанных окружностей треугольников APB , BPC , CPD и DPA лежат на одной окружности (здесь вневписанные окружности пересекают стороны четырёхугольника, в отличие от аналогичного утверждения выше, где вневписанные окружности лежат вне четырёхугольника). Если R m , R n , R k и R l — радиусы вневписанных окружностей APB , BPC , CPD и DPA соответственно, противоположных вершинам B и D , то ещё одним необходимым и достаточным условием того, что четырёхугольник является описанным, будет
Далее выпуклый четырёхугольник, в котором диагонали пересекаются в точке P , является описанным тогда и только тогда, когда
где m , k , n , l – длины сторон AB , BC , CD и DA , а ∆( APB ) — площадь треугольника APB .
Обозначим отрезки, на которые точка P делит диагональ AC как AP = p a и PC = p c . Аналогичным образом P делить диагональ BD на отрезки BP = p b и PD = p d . Тогда четырёхугольник является описанным тогда и только тогда, когда выполняется одно из равенств:
или
или
Условия для описанного четырёхугольника быть другим типом четырёхугольника
Описанный четырёхугольник является ромбом в том и только в том случае, когда противоположные углы равны .
Если вписанная окружность касается сторон AB , BC , CD , DA в точках M , K , N , L соответственно, то ABCD является также вписанным четырёхугольником тогда и только тогда, когда
- хорда MN перпендикулярна KL
Первое утверждение из этих трёх означает, что четырёхугольник касаний MKNL является ортодиагональным .
Описанный четырёхугольник является бицентричным (т.е. описанным и вписанным одновременно) тогда и только тогда, когда радиус вписанной окружности наибольший среди всех описанных четырёхугольников, имеющих ту же самую последовательность длин сторон .
Описанный четырёхугольник является дельтоидом в том и только в том случае, когда любое из нижеследующих условий выполняется:
- Площадь равна половине произведения диагоналей
- Диагонали перпендикулярны
- Два отрезка, соединяющие противоположные точки касания, имеют равные длины
- Одна пара противоположных отрезков от вершины до точки касания имеют одинаковые длины
- Средние линии имеют одинаковые длины
- Произведения противоположных сторон равны
- Центр вписанной окружности лежит на диагонали, являющейся осью симметрии.
См. также
Примечания
- ↑ , с. 119–130.
- ↑ , с. 64–68.
- от 1 марта 2021 на Wayback Machine , §146.
- , с. 65.
- , с. 66.
- ↑ , с. 113–118.
- , с. 72.
- ↑ , с. 28–30.
- , с. 128.
- , с. 103–106.
- , с. 203.
- ↑ . Дата обращения: 1 апреля 2015. 4 марта 2016 года.
- ↑ Yiu, Paul, Euclidean Geometry , (недоступная ссылка) , 1998, pp. 156–157.
- , с. 54–56.
- . Дата обращения: 1 апреля 2015. 20 февраля 2014 года.
- , с. 103–106б Lemma2.
- , с. 239, 242.
- , с. 27–34.
- , с. Lemma3.
- ↑ , с. 124.
- , с. 166.
- , с. 162.
- Gutierrez, Antonio, "Circumscribed Quadrilateral, Diagonal, Chord, Proportion", от 2 апреля 2015 на Wayback Machine , Accessed 2012-04-09.
- , с. 42.
- ↑ , с. Cor.3.
- , с. 289–295.
- , с. Cor.4.
- "Ineq-G126 - Geometry - very nice!!!!", Post at Art of Problem Solving , 2011,
- (недоступная ссылка)
- , с. 462–465.
- .
- , с. 657–658.
- , с. 169.
- ↑ , с. 27–28.
- , с. 70.
- , с. 23–24.
- , с. 72-73.
- ↑ , с. 74.
- , с. 73.
- , с. 79.
- , с. 80.
- , с. 211–212.
- , с. 77.
- , с. 102–107.
- , с. 392-393.
- , с. 165–174.
Ссылки
- Titu Andreescu, Bogdan Enescu. Mathematical Olympiad Treasures. — Birkhäuser, 2006.
- Helen. On a circle attached to a collapsible four-bar // American Mathematical Monthly . — 1926. — Т. 33 , вып. 9 . — .
- Alexander Bogomolny. When A Quadrilateral Is Inscriptible? // Interactive Mathematics Miscellany and Puzzles.
- C.V. Durell, A. Robson. Advanced Trigonometry // Dover reprint. — 2003.
- Victor Bryant, John Duncan. Wheels within wheels // . — 2010. — Вып. 94, November .
- Albrecht Hess. On a circle containing the incenters of tangential quadrilaterals // Forum Geometricorum. — 2014. — Т. 14 .
- Wu Wei Chao, Plamen Simeonov. When quadrilaterals have inscribed circles (solution to problem 10698) // American Mathematical Monthly . — 2000. — Т. 107 , вып. 7 . — doi : .
- Mowaffaq Hajja. A condition for a circumscriptible quadrilateral to be cyclic // Forum Geometricorum. — 2008. — Т. 8 .
Larry Hoehn. A new formula concerning the diagonals and sides of a quadrilateral. — 2011. — Т. 11 .
- John P. Hoyt. Quickies, Q694 // Mathematics Magazine . — 1984. — Т. 57 , вып. 4 .
- John P. Hoyt. Maximizing the Area of a Trapezium // American Mathematical Monthly . — 1986. — Т. 93 , вып. 1 . — doi : .
- Martin Josefsson. Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral // Forum Geometricorum. — 2010a. — Т. 10 .
Martin Josefsson. On the inradius of a tangential quadrilateral // Forum Geometricorum. — 2010b. — Т. 10 .
- Martin Josefsson. Characterizations of Bicentric Quadrilaterals // Forum Geometricorum. — 2010c. — Т. 10 .
- Martin Josefsson. When is a Tangential Quadrilateral a Kite? // Forum Geometricorum. — 2011a. — Т. 11 .
- Martin Josefsson. More Characterizations of Tangential Quadrilaterals // Forum Geometricorum. — 2011b. — Т. 11 .
- Martin Josefsson. The Area of a Bicentric Quadrilateral // Forum Geometricorum. — 2011c. — Т. 11 .
- Martin Josefsson. Similar Metric Characterizations of Tangential and Extangential Quadrilaterals // Forum Geometricorum. — 2012. — Т. 12 .
- Martin Josefsson. Characterizations of Orthodiagonal Quadrilaterals. — 2012b. — Т. 12 .
- Nicusor Minculete. Characterizations of a Tangential Quadrilateral // Forum Geometricorum. — 2009. — Т. 9 .
- Alexei Myakishev. On Two Remarkable Lines Related to a Quadrilateral // Forum Geometricorum. — 2006. — Т. 6 .
- A.W. Siddons, R.T. Hughes. Trigonometry. — Cambridge Univ. Press, 1929.
- И. Вайнштейн, Н. Васильев, В. Сендеров. (Решение задачи) M1495 // Квант. — 1995. — Вып. 6 .
- Michael De Villiers. Equiangular cyclic and equilateral circumscribed polygons // . — 2011. — Вып. 95, March .
Внешние ссылки
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- 2020-09-29
- 1