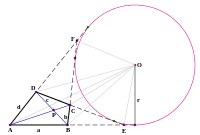
Внеописанный четырёхугольник — это выпуклый четырёхугольник , продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника) . Окружность называется вневписанной . Центр вневписанной окружности лежит на пересечении шести биссектрис. Это биссектрисы двух внутренних углов противоположных углов четырёхугольника, биссектрисы внешних углов двух других вершин, и биссектрисы внешних углов в точках пересечения продолжений противоположных сторон (смотрите рисунок справа, указанные продолжения сторон проведены пунктиром). Внеописанный четырёхугольник тесно связан с описанным четырёхугольником (у которого четыре стороны касаются окружности).

Специальные случаи

Дельтоиды являются примером внеописанных четырёхугольников. Параллелограммы (которые включают квадраты , ромбы и прямоугольники ) можно считать внеописанными четырёхугольниками с бесконечным радиусом вневписанной окружности, поскольку они удовлетворяют свойствам, описанным ниже, но внеописанная окружность не может касаться обеих пар продолжений сторон (ввиду их параллельности) . Выпуклые четырёхугольники, длины сторон которых образуют арифметическую прогрессию , всегда являются внеописанными, поскольку удовлетворяют условиям, описанным ниже для смежных сторон.

Свойства

Выпуклый четырёхугольник является внеописанным тогда и только тогда , когда существует шесть пересекающихся в одной точке биссектрис. Это биссектрисы двух внутренних углов противоположных углов четырёхугольника, биссектрисы внешних углов двух других вершин и биссектрисы внешних углов в точках пересечения продолжений противоположных сторон .

Критерии Штейнера внеописанности четырёхугольника для окружности. Теорема Штейнера

• Теорема Штейнера . С точки зрения вычислений, более полезно свойство, что выпуклый четырёхугольник со сторонами a, b, c, d является внеописанным тогда и только тогда, когда сумма двух смежных сторон равна сумме двух других сторон. Это возможно в двух случаях — либо

${\displaystyle a+b=c+d}$ ,

либо

${\displaystyle a+d=b+c.}$

Свойство доказано Якобом Штейнером в 1846 году . В первом случае вневписанная окружность находится со стороны большего из углов при вершинах A или C , в то время как во втором случае окружность находится со стороны большего из углов при вершинах B или D . Здесь стороны четырёхугольника ABCD имеют длины a = AB , b = BC , c = CD и d = DA . Комбинируя два полученных равенства, получим, что абсолютные величины разностей противоположных сторон равны ,

${\displaystyle |a-c|=|b-d|.}$

Это равенство тесно связано с теоремой Пито для описанных четырёхугольников , по которой суммы противоположных сторон равны.

Критерии Уркхарта внеописанности четырёхугольника для окружности . Теорема Уркхарта.

• . Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F , то для того, чтобы этот четырёхугольник был внеописанным для окружности, необходимымо, чтобы выполнялось любое из двух условий

${\displaystyle AB+BC=AD+DC\quad \Leftrightarrow \quad AE+EC=AF+FC.}$

Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F , то для того, чтобы этот четырёхугольник был внеописанным для окружности, необходимымо и достаточно , чтобы выполнялось любое из двух условий

${\displaystyle AB+BC=AD+DC\quad \Leftrightarrow \quad AE+EC=AF+FC.}$

Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F , то

${\displaystyle AB+BC=AD+DC\quad \Leftrightarrow \quad AE+EC=AF+FC.}$

Вывод слева направо назван именем Л. М. Уркхарта (1902—1966), хотя доказан задолго до него Огастесом де Морганом в 1841 году. Даниэль Педо (Daniel Pedoe) назвал это утверждение самой элементарной теоремой евклидовой геометрии , поскольку в ней речь идёт только о прямых и расстояниях . Эквивалентность доказал Моваффак Хаджа (Mowaffac Hajja) , что сделало равенство справа другим необходимым и достаточным условием для того, чтобы четырёхугольник был внеописанным.

Сравнение с описанным четырёхугольником

Несколько показателей описанных четырёхугольников (левый столбец таблицы) имеют очень похожего двойника для внеописанного четырёхугоольников (средний и правый столбец таблицы), как можно видеть в таблице ниже . Так, выпуклый четырёхугольник имеет вписанную или вневписанную окружность около соответствующей вершины (зависит от столбца) тогда и только тогда, когда выполняется любое из пяти условий.

Вписанная	Вневписанная вне A или C	Вневписанная вне B или D
${\displaystyle R_{1}+R_{3}=R_{2}+R_{4}}$	${\displaystyle R_{1}+R_{2}=R_{3}+R_{4}}$	${\displaystyle R_{1}+R_{4}=R_{2}+R_{3}}$
${\displaystyle agh+cef=beh+dfg}$	${\displaystyle agh+beh=cef+dfg}$	${\displaystyle agh+dfg=beh+cef}$
${\displaystyle {\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{4}}}}$	${\displaystyle {\frac {1}{h_{1}}}+{\frac {1}{h_{2}}}={\frac {1}{h_{3}}}+{\frac {1}{h_{4}}}}$	${\displaystyle {\frac {1}{h_{1}}}+{\frac {1}{h_{4}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{3}}}}$
${\displaystyle \tan {\frac {x}{2}}\tan {\frac {z}{2}}=\tan {\frac {y}{2}}\tan {\frac {w}{2}}}$	${\displaystyle \tan {\frac {x}{2}}\tan {\frac {w}{2}}=\tan {\frac {y}{2}}\tan {\frac {z}{2}}}$	${\displaystyle \tan {\frac {x}{2}}\tan {\frac {y}{2}}=\tan {\frac {z}{2}}\tan {\frac {w}{2}}}$
${\displaystyle R_{a}R_{c}=R_{b}R_{d}}$	${\displaystyle R_{a}R_{b}=R_{c}R_{d}}$	${\displaystyle R_{a}R_{d}=R_{b}R_{c}}$

Обозначения в таблице следующие:

В выпуклом четырёхугольнике ABCD диагонали пересекаются в точке P . R ₁ , R ₂ , R ₃ , R ₄ — радиусы описанных окружностей для треугольников ABP , BCP , CDP , DAP

h ₁ , h ₂ , h ₃ , h ₄ — высоты из точки P на стороны a = AB , b = BC , c = CD , d = DA соответственно в тех же треугольниках

e , f , g , h — расстояния от вершин A , B , C , D до точки P

x , y , z , w — углы ABD , ADB , BDC , DBC соответственно

R _a , R _b , R _c , R _d — радиусы окружностей, внешне касательных сторонам a , b , c , d соответственно и продолжениям смежных двух сторон.

Площадь

Внеописанный четырёхугольник ABCD со сторонами a, b, c, d имеет площадь

${\displaystyle K={\sqrt {abcd}}\sin {\frac {B+D}{2}}.}$

Заметьте, что это та же самая формула, что и для описанного четырёхугольника , и она также вытекает тем же самым образом из соотношения Бретшнайдера .

Радиус вневписанной окружности

Радиус вневписанной окружности четырёхугольника со сторонами a , b , c , d задаётся формулой

${\displaystyle r={\frac {K}{|a-c|}}={\frac {K}{|b-d|}}}$ ,

где K — площадь четырёхугольника. Для четырёхугольника с заданными сторонами максимален , когда четырёхугольник также является вписанным . Эти формулы объясняют, почему все параллелограммы имеют бесконечный радиус вневписанной окружности.

Внешне бицентральный четырёхугольник

Если вокруг внеописанного четырёхугольника можно описать окружность , его называют внебицентральным четырёхугольником . В этом случае, поскольку противоположные углы в сумме составляют 180 °, площадь четырёхугольника можно вычислить по формуле

${\displaystyle \displaystyle K={\sqrt {abcd}}}$ ,

той же самой, что и для .

Если x — расстояние между центром описанной окружности и центром вневписанной окружности, то

${\displaystyle {\frac {1}{(R-x)^{2}}}+{\frac {1}{(R+x)^{2}}}={\frac {1}{r^{2}}},}$

где R — радиус описанной окружности, а r — радиус вневписанной окружности. Это то же самое равенство, что и в для бицентрального четырёхугольника. Однако решая квадратное уравнение относительно x , нужно выбирать другой корень, не тот, что выбирается для бицентрального четырёхугольника. Таким образом, для внеописанного четырёхугольника мы имеем

${\displaystyle x={\sqrt {R^{2}+r^{2}+r{\sqrt {4R^{2}+r^{2}}}}}.}$

Из этой формулы следует, что

${\displaystyle x>R+r}$ ,

что означает, что описанная и вневписанная окружности никогда не могут пересекаться.

См. также

• Полный четырёхугольник
• Вписанный четырёхугольник

Примечания

Литература

• Alexander Bogomolny. // Interactive Mathematics Miscellany and Puzzles. — 1995.
• Martin Josefsson. . — 2012. — Т. 12 .
• Mowaffaq Hajja. // Forum Geometricorum. — 2006. — Т. 6 .
• Kiran S. Kedlaya. . — 2006.
• Mirko Radic, Zoran Kaliman, Vladimir Kadum. A condition that a tangential quadrilateral is also a chordal one // Mathematical Communications. — 2007. — Вып. 12 .