Степень диссоциации — величина, характеризующая состояние равновесия в реакции диссоциации в (однородных) системах .

Определение

Степень диссоциации равна отношению продиссоциированных молекул вещества ${\displaystyle n}$ к общему числу его молекул ${\displaystyle N}$ . Выражается в долях или процентах.

${\displaystyle \alpha ={\frac {n}{N}}\cdot 100\%}$

Степень диссоциации зависит как от природы растворённого электролита, так и от концентрации раствора.

Пример. Для уксусной кислоты CH ₃ COOH величина ${\displaystyle \alpha }$ равна 4% (в 0.01 М растворе). Это значит, что в водном растворе кислоты лишь 4 из каждых 100 молекул диссоциированы, то есть находятся в виде ионов Н ⁺ и СН ₃ СОО ⁻ , остальные же 96 молекул не диссоциированы. Как видно в таком примере, количества частиц, о которых идёт речь в определении степени диссоциации (они же концентрации при условии единичного объёма) - это равновесные количества (концентрации соответственно).

Экспериментальные методы

Степень диссоциации определяется:

• по электропроводности раствора
• по понижению температуры замерзания

Мнимая степень электрической диссоциации

Поскольку сильные электролиты диссоциируют практически полностью, можно было бы ожидать для них изотонический коэффициент , равный количеству ионов (или поляризованных атомов) в формульной единице (молекуле). Однако в действительности этот коэффициент всегда меньше определённого по формуле (например, изотонический коэффициент для 0,05- молярного раствора NaCl равен i = 1,9 вместо 2,0, а (для раствора сульфата магния той же концентрации вовсе i = 1,3). Это объясняет теория сильных электролитов , разработанная в 1923 году П. Дебаем и Э. Хюккелем : передвижение ионов в растворе затруднено образовавшейся оболочкой сольватации. К тому же, ионы взаимодействуют и между собой: разноимённо заряженные притягиваются, а одноимённо заряженные — отталкиваются; силы взаимного притяжения приводят к образованию групп ионов, перемещающихся по раствору совместно. Такие группы называют ионными ассоциатами или ионными па́рами . Соответственно, раствор ведёт себя так, будто содержит меньше частиц, чем на самом деле, ведь свобода их перемещения ограничена. Наиболее очевиден пример, касающийся электропроводности растворов ${\displaystyle \lambda }$ , которая возрастает с разбавлением раствора. Через отношение реальной электропроводности к таковой при бесконечном разбавлении определяют мнимую степень диссоциации сильных электролитов, также обозначаемую через ${\displaystyle \alpha }$ :

${\displaystyle \alpha ={\frac {\lambda }{\lambda _{\infty }}}={\frac {n_{\text{img}}}{n_{\text{disslv.}}}}}$ ,

где ${\displaystyle n_{\text{img}}}$ — мнимое, а ${\displaystyle n_{\text{disslv.}}}$ — реальное количество частиц в растворе.

Связь с константой диссоциации

Из закона разбавления Оствальда следует:

${\displaystyle {\alpha }={\frac {-K+{\sqrt {K^{2}+4CK}}}{2C}}}$

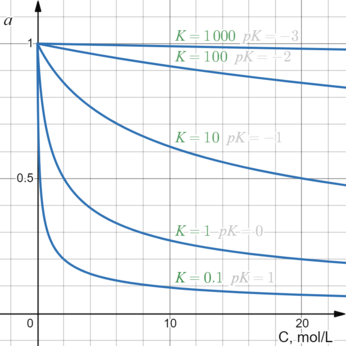
при малых значениях ${\displaystyle \alpha <<1}$ удобно принять

${\displaystyle \alpha \approx {\sqrt {K \over C}}}$

Абсолютная погрешность

${\displaystyle \alpha _{rough}={\sqrt {K \over C}}}$	${\displaystyle \delta ={\alpha _{rough}-\alpha \over \alpha }}$	${\displaystyle {\alpha }={\frac {-K+{\sqrt {K^{2}+4CK}}}{2C}}}$
100%	0.61803398875	61.803398875%
50%	0.2807	39.04%
40%	0.2198	32.79%
30%	0.1612	25.84%
20%	0.1050	18.10%
15%	0.0778	13.92%
10%	0.0512	9.51%
5%	0.0225	4.88%
x	0.5*x + 0.1184*x^2	${\displaystyle {x \over 2}{\left(-x+{\sqrt {x^{2}+4}}\right)}}$

для диссоциации вида A _n B _m = nA + mB

${\displaystyle \alpha ={\sqrt[{n+m}]{K\cdot (1-\alpha) \over n^{n}m^{m}C^{n+m-1}}}\ {\overset {\underset {\mathrm {\alpha <<1} }{}}{\approx }}\ {\sqrt[{n+m}]{K \over n^{n}m^{m}C^{n+m-1}}}}$

Поскольку диссоциация описывается постадийно, данная формула не применяется.

См. также

• Закон разбавления Оствальда
• Константа диссоциации

Примечания

Литература

• Глинка Н. Л. Общая химия — 24-е издание, исправленное. М. 1985. с. 228.