Interested Article - Гравитационный колодец

- 2021-10-25
- 1

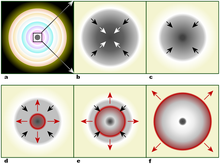
Гравитационный колодец — концепция рассмотрения гравитационного поля небесных тел , интерпретация графика их гравитационного потенциала : чем массивнее тело, тем глубже и больше порождаемый им гравитационный колодец.
Так, Солнце , как самый массивный объект Солнечной системы, порождает в ней самый большой и глубокий колодец . Центр гравитационного колодца, порождаемого телом, совпадает с его центром масс и рассматривается, как его «дно», а процесс высвобождения из гравитационного поля тела — как «вылезание из гравитационного колодца». Чем глубже гравитационный колодец, тем больше энергии требуется, чтобы из него выбраться. Для покидания гравитационного колодца какого-либо тела, надо достичь относительно него второй космической скорости .
В астрофизике гравитационный колодец имеет конкретный смысл поля гравитационного потенциала вокруг массивного тела. Среди других типов потенциальных колодцев рассматриваются электрический и магнитный потенциальные колодцы. Иногда физические модели гравитационных колодцев используются для иллюстраций в небесной механике .
Детали



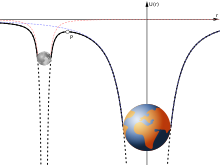
Гравитационный потенциал сферически симметричного тела массы M вне этого тела задаётся формулой
- где G — гравитационная постоянная .
График этой функции на двумерной плоскости ( гиперболоид ) показан справа, с дополнением графиком потенциала внутри тела постоянной плотности, хотя эта часть графика и бессмысленна, поскольку орбита не может пересекать тело.
В культуре
Искусственные гравитационные колодцы являются частым элементом антуража во вселенной « Звёздных войн » .
Примечания
- от 4 февраля 2020 на Wayback Machine (Keith J. Mirenberg) (англ.)
- от 26 мая 2021 на Wayback Machine в Вукипедии
Литература
- Vladimirov, V. S. (1971), Equations of mathematical physics , Translated from the Russian by Audrey Littlewood. Edited by Alan Jeffrey. Pure and Applied Mathematics, vol. 3, New York: Marcel Dekker Inc., MR .
- Wang, W. X. (1988). "The potential for a homogeneous spheroid in a spheroidal coordinate system. I. At an exterior point". J. Phys. A: Math. Gen . 21 (22): 4245-4250. Bibcode : . doi : .
- Milon, T. (1990). "A note on the potential of a homogenous ellipsoid in ellipsoidal coordinates". J. Phys. A: Math. Gen . 23 (4): 581—584. doi : .
- Rastall, Peter. . — World Scientific , 1991. — P. 7ff. — ISBN 981-02-0778-6 .
- Conway, John T. (2000). . Mon. Not. R. Astron. Soc . 316 (3): 555—558. Bibcode : . doi : .
- Cohl, H. S.; Tohline, J. E.; Rau, A. R. P. (2000). "Developments in determining the grativational potential using toroidal functions". Astron. Nachr . 321 (5/6): 363—372. Bibcode : . doi : .
- Thornton, Stephen T.; Marion, Jerry B. (2003), Classical Dynamics of Particles and Systems (5th ed.), Brooks Cole, ISBN 978-0-534-40896-1 .
- Fukushima, Toshio (2014). "Prolate spheroidal harmonic expansion of gravitational field". Astrophys. J . 147 (6): 152. Bibcode : . doi : .
Ссылки
- (англ.) ,
- Zhu, Lupeia . EAS-437 Earth Dynamics . Saint Louis University (1988). Дата обращения: 25 марта 2009.
- Charles D. Ghilani. . Penn State Surveying Engineering Program (28 ноября 2006). Дата обращения: 25 марта 2009. Архивировано из 18 июля 2011 года.
- 2021-10-25
- 1