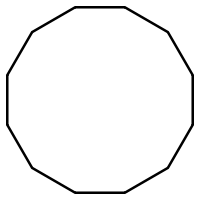
Описанный многоугольник , известный также как тангенциальный многоугольник — это выпуклый многоугольник , который содержит вписанную окружность . Это такая окружность, по отношению к которой каждая сторона описанного многоугольника является касательной . описанного многоугольника — это многоугольник, который имеет описанную окружность , проходящую через все его вершины.

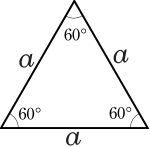
Все треугольники являются описанными для какой-либо окружности, как и все правильные многоугольники с произвольным числом сторон. Хорошо изученная группа описанных многоугольников — описанные четырёхугольники, куда входят ромбы и дельтоиды .

Описания

Выпуклый многоугольник имеет вписанную окружность тогда и только тогда, когда все внутренние биссектрисы его углов (пересекаются в одной точке) и эта общая точка пересечения является центром вписанной окружности .

Описанный многоугольник с n последовательными сторонами ${\displaystyle a_{1},\dots ,a_{n}}$ существует тогда и только тогда, когда система уравнений

${\displaystyle x_{1}+x_{2}=a_{1},\quad x_{2}+x_{3}=a_{2},\quad \ldots ,\quad x_{n}+x_{1}=a_{n}}$

имеет решение ${\displaystyle (x_{1},\dots ,x_{n})}$ в положительных вещественных числах . Если такое решение существует, то ${\displaystyle x_{1},\dots ,x_{n}}$ являются касательными длинами многоугольника (длинами от вершины до точки касания на стороне).

Единственность и неединственность

Если число сторон n нечётно, то для любого заданного набора длин сторон ${\displaystyle a_{1},\dots ,a_{n}}$ , удовлетворяющих критерию выше, существует только один описанный многоугольник. Но если n чётно, существует их бесконечное число . Например, в случае четырёхугольника, когда все стороны равны, мы будем иметь ромб с любой величиной острого угла и все эти ромбы будут описаны вокруг какой-либо окружности.

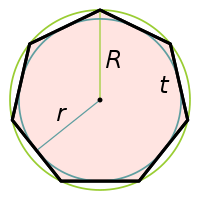
Радиус вписанной окружности

Если длины сторон описанного многоугольника равны ${\displaystyle a_{1},\dots ,a_{n}}$ , то радиус вписанной окружности равен .

${\displaystyle r={\frac {K}{s}}={\frac {2K}{\sum _{i=1}^{n}a_{i}}}}$

где K — площадь многоугольника, а s — его полупериметр . (Поскольку все треугольники имеют вписанную окружность, эта формула применима ко всем треугольникам.)

Другие свойства

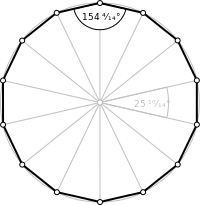
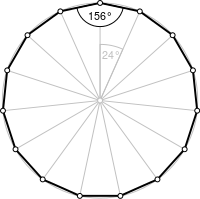
• Для описанного многоугольника с нечётным числом сторон все стороны равны тогда и только тогда, когда углы равны (многоугольник правильный). Описанный многоугольник с чётным числом сторон имеет все стороны равными тогда и только тогда, когда чередующиеся углы равны.
• В описанном многоугольнике с чётным числом сторон сумма длин нечётных сторон равна сумме длин чётных сторон .
• Описанный многоугольник имеет бо́льшую площадь, чем любой другой многоугольник с тем же периметром и теми же внутренними углами в той же последовательности .
• Барицентр любого описанного многоугольника, барицентр его точек границы и центр вписанной окружности коллинеарны и барицентр многоугольника находится между двумя другими указанными центрами и вдвое дальше от центра вписанной окружности, чем от барицентра границы .

Описанный треугольник

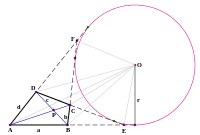
Все треугольники имеют некоторую вписанную окружность. Треугольник называется тангенциальным треугольником рассматриваемого треугольника, если все касания тангенциального треугольника окружности также являются вершинами рассматриваемого треугольника.

Описанный четырёхугольник

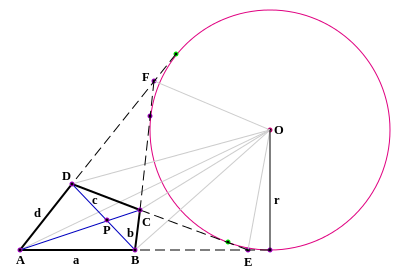
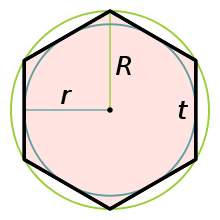
Описанный шестиугольник

• В описанном шестиугольнике ABCDEF главные диагонали AD , BE и CF согласно теореме Брианшона .

Примечания

Литература