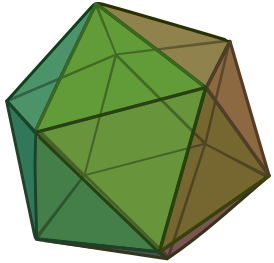
Пра́вильный додека́эдр ( др.-греч. δωδεκάεδρον , от δώδεκα — «двенадцать» и ἕδρα — «грань») — один из пяти возможных правильных многогранников . Додекаэдр составлен из двенадцати правильных пятиугольников , являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).

История

Пожалуй, самый древний предмет в форме додекаэдра был найден в северной Италии , около Падуи , в конце XIX века, он датируется 500 г. до н. э. и предположительно использовался этрусками в качестве игральной кости .

Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различные классические стихии . О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца» . Евклид в предложении 17 книги XIII « Начал » строит додекаэдр на рёбрах куба ^:132-136 . Папп Александрийский в «Математическом собрании» занимается построением додекаэдра, вписанного в данную сферу, попутно доказывая, что вершины додекаэдра лежат в параллельных плоскостях ^:318-319 .

На территории нескольких европейских стран найдено множество предметов, называемых римскими додекаэдрами , относящихся ко II—III вв. н. э., назначение которых не совсем понятно.

Вскоре после появления кубика Рубика , в 1981 году была запатентована подобная головоломка в форме правильного додекаэдра — мегаминкс . Как и у классического кубика Рубика, к каждому ребру у неё прилегает по три детали . Позднее, как и для кубика Рубика появились такие додекаэдрические головоломки с четырьмя деталями при ребре (гигаминкс), пятью (тераминкс) и т.д. Сложность и время сборки их, как и для кубика Рубика возрастает по мере увеличения числа деталей при ребре.

Основные формулы

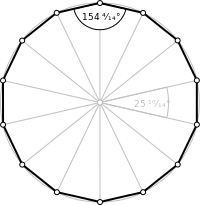
Если за длину ребра принять ${\displaystyle a}$ , то площадь поверхности додекаэдра равна

${\displaystyle S=3a^{2}{\sqrt {5(5+2{\sqrt {5}})}}\approx 20{,}65a^{2}.}$

Объём додекаэдра

${\displaystyle V={\frac {a^{3}}{4}}(15+7{\sqrt {5}})\approx 7{,}66a^{3}.}$

Радиус описанной сферы

${\displaystyle R={\frac {a}{4}}(1+{\sqrt {5}}){\sqrt {3}}\approx 1{,}4012a.}$

Радиус полувписанной сферы равен ${\displaystyle {\frac {3+{\sqrt {5}}}{4}}a\approx 1{,}309a.}$

Радиус вписанной сферы

${\displaystyle r={\frac {a}{4}}{\sqrt {10+{\frac {22}{\sqrt {5}}}}}\approx 1{,}1135a.}$

Свойства

• Все двадцать вершин додекаэдра лежат по пять в четырёх параллельных плоскостях , образуя в каждой из них правильный пятиугольник.
• Двугранный угол между любыми двумя смежными гранями додекаэдра равен arccos(−1/√5) ≈ 116,565° .
• Сумма плоских углов при каждой из 20 вершин равна 324°, телесный (трёхгранный) угол равен arccos(−11/5√5) ≈ 2,9617 стерадиана .
• В додекаэдр можно вписать куб так, что стороны куба будут диагоналями додекаэдра.
• Додекаэдр имеет три звёздчатые формы .
• В додекаэдр можно вписать пять кубов. Если заменить пятиугольные грани додекаэдра плоскими пятиугольными звездами так, что исчезнут все рёбра додекаэдра, то получим пространство пяти пересекающихся кубов. Додекаэдр как таковой исчезнет. Вместо замкнутого многогранника появится открытая геометрическая система пяти ортогональностей. Или симметричное пересечение пяти трёхмерных пространств.
• Ближайшая параллельная к произвольно выбранной грани плоскость, в которой лежат пять вершин, не принадлежащих выбранной грани, отстоит от этой грани на расстояние радиуса описанной вокруг данной грани окружности. А радиус описанной вокруг этих пяти вершин окружности равен диаметру вписанной в любую из граней окружности. Эти две величины равны, соответственно, ${\displaystyle {\sqrt {\frac {5+{\sqrt {5}}}{10}}}a}$ и ${\displaystyle {\frac {{\sqrt {5}}+1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}a}$ , где ${\displaystyle a}$ — длина ребра додекаэдра.

Элементы симметрии додекаэдра

• Додекаэдр имеет центр симметрии и 15 осей симметрии. Каждая из осей проходит через середины противолежащих параллельных рёбер.
• Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.
• Группа вращений додекаэдра обозначается ${\displaystyle I}$ и изоморфна ${\displaystyle A_{5}}$ ( знакопеременная группа степени 5), а полная группа симметрий ${\displaystyle I_{h}}$ изоморфна ${\displaystyle A_{5}\times Z_{2}}$ .

Связь со сферическим замощением

Правильный додэкаэдр также индуцирует замощение сферы правильными пятиугольниками.

	Стереографическая проекция

Интересные факты

• В 1887 году Эрнст Геккель описал радиолярию , имеющую форму, близкую к додекаэдру .
• в 1982 году был синтезирован додекаэдран , химическое соединение (C ₂₀ H ₂₀ ) в форме додекаэдра.
• В 2003 году при анализе данных космического аппарата WMAP , была выдвинута гипотеза, что Вселенная представляет собой додекаэдрическое пространство Пуанкаре .

В культуре

• Додекаэдр применяется как генератор случайных чисел (вместе с другими костями ) в настольных ролевых играх , и обозначается при этом d12 (dice — кости).
• Изготавливаются настольные календари в форме додекаэдра из бумаги, где каждый из двенадцати месяцев расположен на одной из граней .
• В игре Пентакор мир представлен в виде этой геометрической фигуры ^{[ источник не указан 2943 дня ]} .
• В играх «Sonic the Hedgehog 3» и «Sonic & Knuckles» серии Sonic the Hedgehog вид додекаэдра имеют Изумруды Хаоса ^{[ источник не указан 2943 дня ]} .
• В игре «Destiny» форму додекаэдра имеют энграммы ^{[ источник не указан 2943 дня ]} .
• В игре «Overwatch» персонаж Сигма при основной атаке выпускает по 2 додекаэдра ^{[ источник не указан 1420 дней ]} .
• Пульт управления системой освещения Nanoleaf Smart Remote Control .

См. также

• Пентагондодекаэдр — неправильный додекаэдр
• Ромбододекаэдр
• Ромбоикосододекаэдр
• Двенадцатигранники
• Мегаминкс

Примечания

Ссылки

• На Викискладе есть медиафайлы по теме