Interested Article - Простое число

- 2021-07-06
- 2


Просто́е число́ — натуральное число , имеющее ровно два различных натуральных делителя . Другими словами, натуральное число является простым, если оно отлично от и делится без остатка только на и на само .
Пример: число простое (делится на и на ), а не является простым, так как, помимо и , делится на — имеет три натуральных делителя.
Изучением свойств простых чисел занимается теория чисел , а основная теорема арифметики устанавливает в ней их центральную роль: любое целое число , превышающее , либо является простым, либо может быть выражено произведением простых чисел, причём такое представление однозначно с точностью до порядка сомножителей . Единицу не относят к простым числам, так как иначе указанное разложение становится неоднозначным : .
Натуральные числа можно разделить на три класса: единица (имеет один натуральный делитель), простое число (имеет два натуральных делителя), составное число (имеет более двух натуральных делителей) . Как простых, так и составных чисел бесконечно много.
Последовательность простых чисел начинается так:
- 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 , , 61 , , 71 , 73 , 79 , 83 , 89 , 97 , 101 , 103 , 107 , 109 , 113 , 127 , 131 , 137 , 139 , 149 , 151 , , 163 , , 173 , 179 , 181 , , 193 , 197 , 199 , , , , , , 239 , , , 257 , , , , , , 283 , , …
Существуют различные алгоритмы проверки числа на простоту. Например, известный метод перебора делителей , в сравнении с другими примитивный и медленный.
Простые числа широко используются в математике и смежных науках. Во многих алгоритмах информационных технологий , например в асимметричных криптосистемах , используются свойства факторизации целых чисел .
Многие проблемы, касающиеся простых чисел, остаются открытыми .
Существуют обобщения понятия простого числа для произвольных колец и других алгебраических структур .
Множество всех простых чисел обычно обозначают символами или
История
Неизвестно, когда было определено понятие простого числа, однако первые свидетельства относят к верхнему палеолиту, что подтверждается костью Ишанго .
В сохранившихся записях древнеегипетских математиков есть намёки на то, что у них были некоторые представления о простых числах: например, папирус Райнда , относящийся ко второму тысячелетию до нашей эры, содержит таблицу соотношений числа 2 к , представленных суммой трёх или четырёх египетских дробей с единицей в числителе и различных знаменателях. Разложения дробей, знаменатели которых имеют общий делитель, похожи, поэтому египтяне по крайней мере знали разницу между простыми и составными числами .

Самые ранние дошедшие до нас исследования простых чисел принадлежат математикам Древней Греции . Они изобрели решето Эратосфена — алгоритм последовательного нахождения всех простых чисел от 1 до . Опубликованные в приблизительно трёхсотом году до нашей эры « Начала » Евклида содержат важные теоремы о простых числах, включая бесконечность их множества, лемму Евклида и основную теорему арифметики .

Вплоть до XVII века существенных новых работ в области простых чисел не было . В 1640 году Пьер де Ферма сформулировал малую теорему Ферма , затем доказанную Лейбницем и Эйлером , и теорему о сумме двух квадратов , а также высказал предположение: все числа вида являются простыми, и даже доказал это до . Но уже для следующего числа Ферма Эйлер доказал делимость на . Новые простые числа в последовательности Ферма не найдены до сих пор. В то же время французский монах Марен Мерсенн обнаружил, что последовательность , где — простое, даёт также простое число ( числа Мерсенна ).
Работа Эйлера в теории чисел вместила немало сведений о простых. Он показал, что бесконечный числовой ряд — расходящийся. В 1747 году он доказал, что чётные совершенные числа являются значениями последовательности , где сомножитель является числом Мерсенна. В его переписке с Гольдбахом последний изложил свою знаменитую гипотезу о представлении любого чётного числа, начиная с четырёх, суммой двух простых . Доказательство гипотезы пока не найдено.
С начала XIX века внимание многих математиков занимала проблема асимптотического распределения простых чисел . Лежандр и Гаусс независимо друг от друга высказали предположение: плотность простых чисел в среднем близка к величине, обратно пропорциональной натуральному логарифму .
Долгое время простые числа считались малоприменимыми за пределами чистой математики . Ситуация изменилась в 1970-е годы, после появления концепций криптографии с открытым ключом , в которых простые числа составили основу первых алгоритмов шифрования, таких как RSA .
Разложение натуральных чисел в произведение простых
Представление натурального числа в виде произведения простых называется разложением на простые , или факторизацией числа . На настоящий момент не известны полиномиальные алгоритмы факторизации чисел, хотя и не доказано, что таких алгоритмов не существует. На предполагаемой большой вычислительной сложности задачи факторизации базируется криптосистема RSA и некоторые другие. Факторизация с полиномиальной сложностью теоретически возможна на квантовом компьютере с помощью алгоритма Шора .
Основная теорема арифметики
Основная теорема арифметики утверждает, что каждое натуральное число , большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей . Таким образом, простые числа являются элементарными «строительными блоками» натуральных чисел. Например:
-
. ( обозначает квадратную или вторую степень .)
Как было показано в этом примере, один и тот же простой делитель может появляться несколько раз. Разложение:
- n = p 1 · p 2 · ... · p t
числа n на (конечное число) простых множителей p 1 , p 2 , … , p t называется разложением на простые множители числа n . Основная теорема арифметики может быть перефразирована таким образом: любое разложение на простые числа будет тождественным с точностью до порядка делителей . На практике для большинства чисел есть много простых алгоритмов разложения на множители, все они дают один и тот же результат .
Простота единицы
Большинство древних греков даже не считало числом, поэтому они не могли считать его простым . К Средним векам и эпохе Возрождения многие математики включали в качестве первого простого числа . В середине XVIII века Христиан Гольдбах внёс в список в качестве первого простого числа в своей знаменитой переписке с Леонардом Эйлером ; однако сам Эйлер не считал простым числом . В XIX веке многие математики по-прежнему считали число простым числом. Например, список простых чисел Деррика Нормана Лемера до числа, переизданный в 1956 году, начинался с в качестве первого простого числа. Говорят, что Анри Лебег является последним математиком, который назвал простым . К началу XX века математики стали приходить к консенсусу о том, что не является простым числом, а скорее формирует свою специальную категорию — «единицу» .
Если считать простым числом, то основная теорема Евклида об арифметике (упомянутая выше) не будет выполняться, как было указано в начале статьи. Например, число может быть разложено как 3 · 5 и 1 · 3 · 5 . Если бы являлась простым числом, эти два варианта считались бы разными факторизациями ; следовательно, утверждение этой теоремы пришлось бы изменить . Точно так же решето Эратосфена работало бы неправильно, если бы считалась простым: модифицированная версия решета, которая предполагает, что является простым числом, исключает все множители, кратные (то есть все остальные числа), и даёт на выходе только одно число — . Кроме того, простые числа имеют несколько свойств, которых нет у числа , такие как отношение числа к его соответствующему значению функции тождества Эйлера или суммы функции делителей .
Алгоритмы поиска и распознавания простых чисел

Простые способы нахождения начального списка простых чисел вплоть до некоторого значения дают решето Эратосфена , решето Сундарама и решето Аткина .
Однако, на практике вместо получения списка простых чисел зачастую требуется проверить, является ли данное число простым. Алгоритмы, решающие эту задачу, называются тестами простоты . Существует множество полиномиальных тестов простоты, но большинство их является вероятностными (например, тест Миллера — Рабина ) и используются для нужд криптографии . В 2002 году было доказано, что задача проверки на простоту в общем виде полиномиально разрешима, но предложенный детерминированный тест Агравала — Каяла — Саксены имеет довольно большую вычислительную сложность , что затрудняет его практическое применение .
Для некоторых классов чисел существуют специализированные эффективные тесты простоты (см. ниже).
Тест простоты
Тестом простоты (или проверкой простоты) называется алгоритм , который, приняв на входе число, позволяет либо не подтвердить предположение о составности числа, либо точно утверждать его простоту. Во втором случае он называется истинным тестом простоты. Задача теста простоты относится к классу сложности P , то есть время работы алгоритмов её решения зависит от размера входных данных полиномиально, что было доказано в 2002 году . Появление полиномиального алгоритма предсказывалось существованием полиномиальных сертификатов простоты и, как следствие, тем, что задача проверки числа на простоту принадлежала классам NP и co-NP одновременно.
Существующие алгоритмы проверки числа на простоту могут быть разделены на две категории: истинные тесты простоты и вероятностные тесты простоты. Результатом вычислений истинных тестов всегда является факт простоты либо составности числа. Вероятностный тест показывает, является ли число простым с некоторой вероятностью. Числа, удовлетворяющие вероятностному тесту простоты, но являющиеся составными, называются псевдопростыми . Одним из примеров таких чисел являются числа Кармайкла .
Одним из примеров истинных тестов простоты является тест Люка-Лемера для чисел Мерсенна . Очевидный недостаток этого теста заключается в его применимости только к числам определённого вида. Среди других примеров можно привести основанные на малой теореме Ферма
- Тест Пепина для чисел Ферма
- Теорема Прота для чисел Прота
- Тест Агравала — Каяла — Саксены , первый универсальный, полиномиальный, детерминированный и безусловный тест простоты.
- Тест Люка — Лемера — Ризеля
А также:
- метод перебора делителей
- Теорема Вильсона
- Критерий Поклингтона
- Тест Миллера
- Тест Адлемана — Померанса — Румели , усовершенствованный Коэном и Ленстрой
- Тест простоты с использованием эллиптических кривых .
К вероятностным тестам простоты относят:
- Тест Ферма
- Тест Миллера — Рабина
- Тест Соловея — Штрассена
- Тест Бейли — Померанца — Селфриджа — Уогстаффа
Большие простые числа
Уже в течение многих столетий поиск «больших» простых чисел вызывает интерес математиков. В последние десятилетия эти исследования приобрели прикладное значение из-за применения таких чисел в ряде алгоритмов шифрования, таких как RSA .
В семнадцатом столетии Марен Мерсенн предположил, что числа вида простые (при n ≤ 257) только для n равных 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 и 257 . Проверка верности предположения была намного выше возможностей того времени. Только в XX веке было обнаружено, что гипотеза была ложной и, вероятно, сделана «слепо», поскольку Мерсенн не учел три случая (для n = 61, 89 и 107); кроме того, оказалось, что числа, соответствующие n = 67 и n = 257 — составные .
В 1876 году Эдуард Люка доказал, что число M 127 (39-значное число) — простое, оно оставалось самым большим известным простым числом до 1951 года, когда были найдены (44 цифры) и, немного позднее, (из 79 цифр) — последнее простое число, которое было найдено с помощью электронного калькулятора. С тех пор все последующие большие простые числа были обнаружены с помощью компьютера: с 1952 года (когда SWAC показал, что M 521 является простым), по 1996 год они были найдены суперкомпьютером , и все были простыми Мерсенна (найденные с использованием теста Люка-Лемера , специфического алгоритма для таких чисел), за исключением числа , которое было рекордом между 1989 и 1992 годами .
Алгоритмы получения простых чисел
Некоторые задачи математики с использованием факторизации требуют ряд очень больших простых чисел, выбранных случайным образом. Алгоритм их получения, основанный на постулате Бертрана (Для любого натурального n ≥ 2 найдётся простое число p в интервале n < p < 2 n .) :
Алгоритм:
|
Время решения задачи этим алгоритмом не определено, но есть большая вероятность, что оно всегда является полиномиальным, пока имеется достаточно простых чисел, и они распределены более-менее равномерно . Для простых случайных чисел эти условия выполняются .
Наиболее эффективным средством построения простых чисел является несколько модифицированная малая теорема Ферма .
Пусть N, S — нечётные натуральные числа, N-1 = S*R, причем для каждого простого делителя q числа S существует целое число такое, что
,
Тогда каждый простой делитель p числа N удовлетворяет сравнению
Следствие. Если выполнены условия теоремы Ферма и , то N — простое число .
Покажем теперь, как с помощью последнего утверждения, имея большое простое число , можно построить существенно большее простое число . Выберем для этого случайным образом чётное число на промежутке и положим . Затем проверим число на отсутствие малых простых делителей, разделив его на малые простые числа; испытаем некоторое количество раз с помощью алгоритма Рабина. Если при этом выяснится, что — составное число, следует выбрать новое значение и опять повторить вычисления. Так следует делать до тех пор, пока не будет найдено число N, выдержавшее испытание алгоритмом Рабина достаточно много раз. В этом случае появляется надежда на то, что — простое число, и следует попытаться доказать простоту с помощью тестов простоты .
Бесконечность множества простых чисел
Простых чисел бесконечно много. Это утверждение упоминается как теорема Евклида в честь древнегреческого математика Евклида , поскольку первое известное доказательство этого утверждения приписывается ему. Известно ещё много доказательств бесконечности простых чисел, в том числе аналитическое доказательство Эйлера , доказательство Гольдбаха на основе чисел Ферма , доказательство Фурстенберга с использованием общей топологии и элегантное доказательство Куммера .
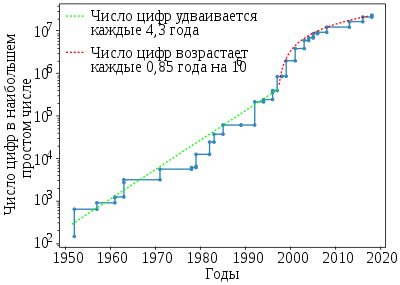
Наибольшее известное простое
Издавна ведутся записи, отмечающие наибольшие известные на то время простые числа . Один из рекордов поставил в своё время Эйлер , найдя простое число 2 31 − 1 = 2 147 483 647 .
Наибольшим известным простым числом по состоянию на январь 2019 года является число Мерсенна M 82 589 933 = 2 82 589 933 − 1 . Оно содержит 24 862 048 десятичных цифр ; в книге с записью этого числа было бы около девяти тысяч страниц. Его нашли 7 декабря 2018 года в рамках проекта по распределённому поиску простых чисел Мерсенна GIMPS . Предыдущее самое большое известное простое число, открытое в декабре 2017 года, было на 1 612 623 знака меньше .
Числа Мерсенна выгодно отличаются от остальных наличием эффективного теста простоты : теста Люка — Лемера . Благодаря ему простые числа Мерсенна давно удерживают рекорд как самые большие известные простые.
За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр EFF назначила денежные призы соответственно в 150 000 и 250 000 долларов США . Ранее EFF уже присуждала призы за нахождение простых чисел из 1 000 000 и 10 000 000 десятичных цифр.
Простые числа специального вида
Существует ряд чисел, простота которых может быть установлена эффективно с использованием специализированных алгоритмов.
- Числа Мерсенна — числа вида , где n — натуральное число . При этом число Мерсенна может быть простым, только если n — простое число. Как уже было отмечено выше, эффективным тестом простоты является тест Люка — Лемера .
- Числа Ферма — числа вида , где n — неотрицательное целое число . Эффективным тестом простоты является тест Пепина . По состоянию на февраль 2015 года известно только 5 простых чисел Ферма (для n = 0, 1, 2, 3, 4), двадцать восемь следующих чисел Ферма (до включительно) оказались составными , однако не доказано, что других простых чисел Ферма нет .
- Числа Вудала — числа вида . Эффективным тестом простоты является тест Люка — Лемера — Ризеля .
- Числа Каллена — числа вида .
- Числа Прота — числа вида , причём k нечётно и . Эффективным тестом простоты для чисел Прота является ( англ. Brillhart–Lehmer–Selfridge test ) . Числа Каллена и числа Ферма являются частным случаем чисел Прота (соответственно при k = n и при k = 1, ) .
- Числа Миллса — числа вида где — константа Миллса .
Для поиска простых чисел обозначенных типов в настоящее время используются проекты распределённых вычислений GIMPS , PrimeGrid , , Seventeen or Bust , , .
Некоторые свойства
- Если p — простое, и p делит ab , то p делит a или b . Доказательство этого факта было дано Евклидом и известно как лемма Евклида . Она используется в доказательстве основной теоремы арифметики .
- Кольцо вычетов является полем тогда и только тогда, когда — простое .
- Характеристика каждого поля — это ноль или простое число .
- Если — простое, а — натуральное, то делится на ( малая теорема Ферма ) .
- Если — конечная группа, порядок которой делится на , то содержит элемент порядка ( теорема Коши ) .
- Если — конечная группа, и — максимальная степень , которая делит , то имеет подгруппу порядка , называемую силовской подгруппой , более того, количество силовских подгрупп равно для некоторого целого ( теоремы Силова ) .
- Натуральное является простым тогда и только тогда, когда делится на ( теорема Вильсона ) .
- Если — натуральное, то существует простое , такое, что ( постулат Бертрана ) .
-
Ряд чисел, обратных к простым
, расходится
. Более того, при
- Любая арифметическая прогрессия вида , где — целые взаимно простые числа , содержит бесконечно много простых чисел ( теорема Дирихле о простых числах в арифметической прогрессии ) .
- Всякое простое число, большее 3, представимо в виде или , где — некоторое натуральное число. Отсюда, если разность между несколькими последовательными простыми числами (при k>1) одинакова, то она обязательно кратна 6 — например: 251-257-263-269; 199-211-223; 20183-20201-20219.
- Если — простое, то кратно 24 (справедливо также для всех нечётных чисел, не делящихся на 3) .
- Теорема Грина-Тао . Существуют сколь угодно длинные конечные арифметические прогрессии, состоящие из простых чисел .
- Никакое простое число не может иметь вид , где n >2, k >1. Иначе говоря, число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, бо́льшим 2. Из этого следует также, что если простое число имеет вид , то k — простое (см. числа Мерсенна ) .
- Никакое простое число не может иметь вид , где n >1, k >0. Иначе говоря, число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, бо́льшим 1 .
- Каждое простое число (кроме чисел вида ) можно представить в виде суммы трех квадратов .
Применения
Простые числа являются фундаментальными компонентами во многих областях математики .
Арифметические функции
Арифметические функции , а именно функции, определённые на множестве натуральных чисел и принимающих значения во множестве комплексных чисел, играют решающую роль в теории чисел. В частности, среди них наиболее важными являются мультипликативные функции, то есть функции , обладающие следующим свойством: если пара состоит из взаимно простых чисел, то имеет место равенство
Примерами мультипликативных функций являются функция Эйлера , которая ставит в соответствие числу количество натуральных чисел, меньших n и взаимно простых с ним и количество делителей числа n . Значение этих функций от степени простого числа:
Арифметические функции можно легко вычислить, зная значения, которые они принимают для степеней простых чисел . На самом деле из разложения натурального числа n на множители
мы имеем, что
и следовательно, возвращаясь к задаче вычисления получается что вычислить от каждой степени простого делителя обычно проще, чем вычислить по общей формуле .
Например, чтобы узнать значение функции Эйлера от n = 450 = 2 × 3 2 × 5 2 , достаточно вычислить
Модульная арифметика
В модульной арифметике простые числа играют очень важную роль: кольцо вычетов является полем тогда и только тогда, когда n является простым . Также существование первообразного корня кольца привязано к простым числам: оно существует, только если n — простое число, 1, 2, 4 или число в форме , где p нечётно.
Одной из важнейших теорем модульной арифметики является малая теорема Ферма . Эта теорема утверждает, что для любого простого числа р и любого натурального числа a имеем:
или для любого простого р и любого натурального а не делящегося на р , справедливо:
Это свойство можно использовать для проверки того, что число не является простым. На самом деле, если n таково, что:
для некоторого натурального а , то n не может быть простым . Однако это свойство не может быть использовано для проверки числа на простоту: есть некоторые числа, называемые числами Кармайкла (наименьшее — 561) для которых это будет неверно. Числом Кармайкла называется составное число, которое является псевдопростым числом по каждому основанию b, взаимно простому с n. В 1994 году Уильям Роберт Альфорд, Эндрю Гранвиль и Карл Померанс показали, что таких чисел бесконечно много .
Теория групп
Простые числа также играют основополагающую роль в алгебре . В теории групп группа, в которой каждый элемент является степенью простого числа р , называется р-группой . P-группа является конечной тогда и только тогда, когда порядок группы (число её элементов) является степенью р. Примером бесконечной р-группы является p -группа Прюфера . Известно, что p- группы имеют нетривиальный центр и, следовательно, не могут быть простыми (кроме группы с p элементами); если группа конечна, более того, все нормальные подгруппы пересекают центр нетривиальным образом.
Примером таких групп является циклическая группа умножения по модулю простого числа .
Все группы порядка p являются циклическими и поэтому абелевыми ; также абелева каждая группа порядка p 2 . Кроме того, любая конечная абелева группа изоморфна прямому произведению конечного числа циклических р-групп.
В теореме Коши утверждается, что если порядок конечной группы G делится на простое число p, то G содержит элементы порядка p. Эта теорема обобщается теоремами Силова .
Криптосистема с открытым ключом
Некоторые алгоритмы криптографии с открытым ключом, такие как RSA и обмен ключами Диффи-Хеллмана , основаны на больших простых числах (обычно 1024—2048 бит). RSA полагается на предположение, что намного проще (то есть более эффективно) выполнять умножение двух (больших) чисел x и y, чем вычислять взаимно простые x и y , если известно только их произведение . Обмен ключами Диффи-Хеллмана основан на том, что существуют эффективные алгоритмы возведения в степень по модулю , а обратная операция — дискретного логарифмирования считается сложной .
RSA
Трудность факторизации больших чисел привела к разработке первого эффективного метода криптографии с открытым ключом — RSA . В этой криптографической системе, человек, который должен получить зашифрованное сообщение, генерирует ключ: выбираются два различных случайных простых числа и заданного размера (обычно используются, 1024- или 2048- битные числа). Далее вычисляется их произведение , называемое модулем . Вычисляется значение функции Эйлера от числа : . Выбирается целое число ( ), взаимно простое со значением функции . Обычно в качестве берут небольшие простые числа (например, простые числа Ферма ). Число называется открытой экспонентой ( англ. public exponent ). Вычисляется число , называемое секретной экспонентой, мультипликативно обратное к числу e по модулю . Пара публикуется в качестве открытого ключа RSA ( англ. RSA public key ). Пара играет роль закрытого ключа RSA ( англ. RSA private key ) и держится в секрете .
Теоретически можно получить закрытый ключ из общедоступной информации: в настоящее время для этого требуется факторизация числа , что делает передачу защищенного сообщения безопасной, если простые числа удовлетворяют определённым условиям и являются «достаточно большими». Пока не известно, существуют ли эффективные методы для расшифровки сообщения, не связанные с прямой атакой на факторизацию , но было показано, что плохой выбор открытого ключа может сделать систему более уязвимой для таких атак .
В 1991 году опубликовала список полупростых чисел, предлагая денежные призы за разложение некоторых из них на множители, с целью подтверждения безопасности метода и поощрения исследования в этой области: инициатива называлась . На протяжении многих лет некоторые из этих чисел были разложены, а для других проблема факторизации все ещё остается открытой; однако конкурс был завершен в 2007 году .
Формулы для нахождения простых чисел
В разное время предпринимались попытки указать выражение, значениями которого при разных значениях входящих в него переменных были бы простые числа . Л. Эйлер указал многочлен принимающий простые значения при n = 0, 1, 2, …, 40 . Однако при n = 41 значение многочлена является составным числом. Можно доказать, что не существует многочлена от одной переменной n , который принимает простые значения при всех целых n . П. Ферма предположил, что все числа вида 2 2 k + 1 простые; однако Эйлер опроверг эту гипотезу, доказав, что число 2 2 5 + 1 = 4 294 967 297 — составное .
Тем не менее, существуют многочлены, множество положительных значений которых при неотрицательных значениях переменных совпадает с множеством простых чисел. Одним из примеров является многочлен
содержащий 26 переменных и имеющий степень 25. Наименьшая степень для известных многочленов такого типа — 5 при 42 переменных; наименьшее число переменных — 10 при степени около 1,6·10 45 . Этот результат является частным случаем доказанной Юрием Матиясевичем диофантовости любого перечислимого множества .
Интересно, что приведённый выше многочлен, который порождает простые числа, сам разлагается на множители. Заметим, что второй множитель этого многочлена (в фигурных скобках) имеет форму: единица минус сумма квадратов. Таким образом, многочлен может принимать положительные значения (при положительных ) только если, каждый из этих квадратов (то есть каждый многочлен в квадратных скобках) равен нулю. В этом случае выражение в фигурных скобках будет равно 1 .
Открытые вопросы

До сих пор существует много открытых вопросов относительно простых чисел, наиболее известные из которых были перечислены Эдмундом Ландау в 1912 году на Пятом Международном математическом конгрессе :
- Проблема Гольдбаха ( первая проблема Ландау ): верно ли, что каждое чётное число, большее двух, может быть представлено в виде суммы двух простых чисел?
- Вторая проблема Ландау : бесконечно ли множество « простых близнецов » — пар простых чисел, разность между которыми равна 2 ? В 2013 году математик Чжан Итан из университета Нью-Гэмпшира доказал, что существует бесконечно большое количество пар простых чисел, расстояние между которыми не превышает 70 миллионов . Другими словами, всегда будут встречаться простые числа, удалённые друг от друга не более чем на 70 млн. Уже 20 июля 2013 года усилиями удалось снизить оценку расстояния до 4680 . В ноябре того же года Джеймс Мэйнард улучшил результат до 600 . Используя идеи Мэйнарда в 2014 году проект Polymath под руководством Теренса Тао несколько улучшили последний метод, гарантируя бесконечное число пар простых чисел с расстоянием не более 246 .
- Гипотеза Лежандра ( третья проблема Ландау ): верно ли, что для всякого натурального числа между и всегда найдётся простое число ?
- Четвёртая проблема Ландау : бесконечно ли множество простых чисел вида , где — натуральное число ?
Открытой проблемой является также существование бесконечного количества простых чисел во многих целочисленных последовательностях, включая числа Мерсенна , числа Фибоначчи , числа Ферма и др.
Вариации и обобщения
Неприводимые и простые элементы
В начале статьи было дано определение простого числа: натуральное число называется простым, если у него ровно два делителя — единица и само число. Аналогичное понятие можно ввести и в других алгебраических структурах; чаще всего рассматривается коммутативные кольца без делителей нуля ( области целостности ) . У таких колец, однако, могут быть делители единицы , образующие мультипликативную группу . Например, в кольце целых чисел существуют два делителя единицы: и Поэтому все целые числа, кроме делителей единицы, имеют не два, а по меньшей мере четыре делителя; например, у числа 7 делителями являются Это означает, что обобщение понятия простого числа должно опираться на иные его свойства.
Аналогом простого числа для области целостности является неприводимый элемент , который определяется следующим образом .
|
Ненулевой элемент области целостности называется неприводимым (иногда неразложимым ), если он не является делителем единицы и из равенства следует, что или является делителем единицы. |
Для целых чисел это определение означает, что неприводимыми элементами являются простые натуральные числа, а также противоположные им.
Из определения следует, что множество делителей неприводимого элемента состоит из двух частей: все делители единицы и произведения на все делители единицы (эти произведения называются элементами, ассоциированными с ). То есть количество делителей неприводимого если оно конечно, вдвое больше количества делителей единицы в кольце.
Важное значение имеет аналог основной теоремы арифметики , который в обобщённом виде формулируется следующим образом :
|
Кольцо называется факториальным , если в нём каждый ненулевой элемент, не являющийся делителем единицы, может быть представлен в виде произведения неприводимых элементов, причём это представление единственно с точностью до перестановки сомножителей и их ассоциированности (умножения на делители единицы). |
Не всякая область целостности факториальна, см. контрпример . Евклидово кольцо всегда факториально .
Существует другое, более узкое обобщение понятия простого числа, называемое простым элементом .
|
Ненулевой элемент области целостности называется простым , если он не является делителем единицы и произведение может делиться на лишь в том случае, когда хотя бы один из элементов или делится на . |
Простой элемент всегда неприводим. В самом деле, если элемент простой и то по определению простого элемента один из сомножителей, пусть это будет делится на то есть Тогда или, сокращая на (в области целостности сокращение ненулевого множителя всегда возможно): то есть является делителем единицы. ■
Обратное, вообще говоря, неверно, неприводимый элемент может не быть простым, если кольцо не является факториальным. Пример : рассмотрим кольцо чисел вида где — целые числа. Число 3 в нём неприводимо, так как у него только 4 делителя: . Однако оно не является простым элементом, в чём убеждает равенство:
Число 3 делит правую часть равенства, но не делит ни одного из сомножителей. Можно из этого факта сделать вывод, что рассмотренное кольцо не факториально; и в самом деле, равенство показывает, что разложение на неприводимые множители в этом кольце не однозначно.
Примеры
Кольцо целых чисел факториально. В нём, как уже упоминалось выше, два делителя единицы.
Гауссовы целые числа
Кольцо гауссовых чисел состоит из комплексных чисел вида где — целые числа. Делителей единицы четыре: Это кольцо факториально, неприводимыми элементами являются часть обычных простых чисел и «простые гауссовы» (например, ). См. критерий простоты гауссова числа .
Пример разложения для числа 2, которое в кольце гауссовых чисел не является простым: — неединственность разложения здесь кажущаяся, поскольку ассоциирована с , согласно равенству:
Целые числа Эйзенштейна
Кольцо целых чисел Эйзенштейна состоит из комплексных чисел следующего вида :
- где — целые числа, ( кубический корень из единицы ),
В этом кольце шесть делителей единицы: (±1, ±ω, ±ω 2 ), оно евклидово и поэтому факториально. Неприводимые элементы (они же простые элементы) кольца называются простыми числами Эйзенштейна.
Критерий простоты : целое число Эйзенштейна является простым числом Эйзенштейна тогда и только тогда, когда выполняется одно из следующих взаимоисключающих условий:
- ассоциировано с натуральным простым числом вида
- (норма ) является натуральным простым вида или .
Отсюда следует, что норма любого целого числа Эйзенштейна является либо простым натуральным числом, либо квадратом простого натурального числа .
Числа, ассоциированные или комплексно-сопряжённые с простыми числами Эйзенштейна, также являются простыми числами Эйзенштейна.
Кольцо многочленов
Большое значение в алгебре имеет кольцо многочленов , образованное многочленами с коэффициентами из некоторого поля Делителями единицы являются здесь ненулевые константы (как многочлены нулевой степени). Кольцо многочленов евклидово и поэтому факториально. Если в качестве взять поле вещественных чисел , то неприводимыми будут все многочлены 1-й степени и те многочлены 2-й степени, у которых нет вещественных корней (то есть их дискриминант отрицателен) .
См. также
Примечания
- ↑ Простое число // . — М. : Советская Энциклопедия , 1977. — Т. 4. 21 января 2022 года.
- ↑ " от 24 февраля 2021 на Wayback Machine ». (англ.)
- Последовательность в OEIS . См. также список простых чисел
- Гарднер, Мартин . От мозаик Пенроуза к надёжным шифрам = Penrose Tiles to Trapdoor Ciphers / пер. с англ. Ю. А. Данилова. — М. : Мир , 1993. — 416 с. — 10 000 экз. — ISBN 5-03-001991-X .
- Elementary Methods in Number Theory. — Springer, 2000. — Vol. 195. — ISBN 978-0-387-22738-2 .
- Faticoni, Theodore G. . — 2nd. — John Wiley & Sons, 2012. — Vol. 111. — P. 44. — ISBN 978-1-118-24382-4 .
- (фр.) (недоступная ссылка) . Site de l’IREM de La Réunion. Voir aussi от 22 декабря 2017 на Wayback Machine , analyse par O. Keller sur Bibnum
- // Mathpages. 1 апреля 2016 года.
- ↑ Рыбников К. // Успехи математических наук . — Российская академия наук , 1941. — № 9 . — С. 318—321 .
- John J. O'Connor, Edmund F. Robertson. (англ.) . MacTutor .
- . Great Internet Mersenne Prime Search . 15 марта 2016 года.
- ↑ Apostol, Tom M. . — New York: Springer-Verlag, 1976. — xii, 338 pages с. — ISBN 0387901639 . 28 апреля 2020 года.
- ↑ Du Sautoy, Marcus. . — Milano: Rizzoli, 2005. — 606 p. с. — ISBN 8817008435 .
- ↑ Menezes, A. J. (Alfred J.), 1965-. . — Boca Raton: CRC Press, 1997. — xxviii, 780 pages с. — ISBN 9780849385230 .
- ↑ Ишмухаметов Ш. Т. Методы факторизации натуральных чисел: учебное пособие // Казань: Казанский университет. — 2011. — С. 190 .
- Dudley, Underwood (1978), Elementary number theory (2nd ed.), W. H. Freeman and Co., ISBN 978-0-7167-0076-0 , Section 2, Theorem 2 (англ.)
- См, например, David E. Joyce’s комментарий на Начала (Евклид) , от 5 августа 2011 на Wayback Machine .
- ↑ от 19 апреля 2015 на Wayback Machine (англ.)
- See for instance: L. Euler. Commentarii academiae scientiarum Petropolitanae 9 (1737), 160—188. Variae observationes circa series infinitas, от 5 октября 2013 на Wayback Machine (англ.)
- Derbyshire, John (2003), "The Prime Number Theorem", Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics , Washington, D.C.: Joseph Henry Press, p. 33, ISBN 978-0-309-08549-6 , OCLC (англ.)
- David Gries, Jayadev Misra. A Linear Sieve Algorithm for Finding Prime Numbers. — 1978.
- Knuth, Donald Ervin, 1938-. . — Reading, Mass.: Addison-Wesley Pub. Co, ©1973-©1981. — 4 volumes с. — ISBN 0201896842 . 15 июня 2020 года.
- ↑ Vasilenko, O. N. (Oleg Nikolaevich). . — Moskva: MT︠S︡NMO. Moskovskiĭ t︠s︡entr nepreryvnogo matematicheskogo obrazovanii︠a︡, 2006. — 333 pages с. — ISBN 5940571034 .
- Б. Шнайер. Прикладная криптография. — С. 296—300.
- Кормен Т., Лейзер Ч. Алгоритмы. Построение и анализ. — М. : МЦНМО, 2002. — С. 765—772.
- Crandall R., Pomerance C. Prime Numbers: A Computational Perspective. — Springer, 2005.
- . — 2nd ed. — Cambridge, Mass.: MIT Press, 2001. — xxi, 1180 pages с. — ISBN 0262032937 . 29 января 2010 года.
- ↑ Нестеренко Ю. В. Введение в криптографию. — Питер, 2001. — 288 с.
- Chris Caldwell. (англ.) . The Prime Pages . Дата обращения: 8 марта 2010. 19 августа 2013 года.
- Jitsuro Nagura. (EN) // Proceedings of the Japan Academy. — 1952. — Т. 28 , вып. 4 . — С. 177—181 . — ISSN . — doi : . 17 ноября 2017 года.
- от 11 июня 2015 на Wayback Machine in Латынь from Goldbach to Euler, July 1730.
- . Дата обращения: 8 марта 2010. 19 августа 2013 года.
- Starr, Michelle. . ScienceAlert (англ.) . из оригинала 6 января 2018 . Дата обращения: 6 января 2018 .
- от 9 ноября 2008 на Wayback Machine (англ.)
- Юлия Рудый. . Вести.Ru (7 февраля 2013). Дата обращения: 25 февраля 2018. 26 февраля 2018 года.
- ↑ Последовательность в OEIS
- Последовательность в OEIS : простые числа Мерсенна
- Последовательность в OEIS
- Keller, Wilfrid (February 15, 2015), , ProthSearch.net , из оригинала 10 февраля 2016 , Дата обращения: 1 марта 2016 от 10 февраля 2016 на Wayback Machine
- Виолант-и-Хольц, Альберт. Загадка Ферма. Трёхвековой вызов математике. — М. : Де Агостини, 2014. — С. 78. — 151 с. — (Мир математики: в 45 томах, том 9). — ISBN 978-5-9774-0625-3 .
- Последовательность в OEIS
- Последовательность в OEIS : простые числа Вудала
- Последовательность в OEIS
- Последовательность в OEIS : простые числа Каллена
- Последовательность в OEIS
- ; Derrick Henry Lehmer ; . (англ.) // : journal. — 1975. — April ( vol. 29 ). — P. 620—647 . — doi : . 4 марта 2016 года.
- Последовательность в OEIS : простые числа Прота
- Caldwell, Chris K.; Cheng, Yuanyou (2005), , Journal of Integer Sequences , 8 (5.4.1) от 5 июня 2011 на Wayback Machine
- Dudley, Underwood (1978), Elementary number theory (2nd ed.), W. H. Freeman and Co., ISBN 978-0-7167-0076-0 , Section 2, Lemma 5 (англ.)
- ↑ Степанов С. А. . — М. : «Знание», 1975. — 64 с. 24 августа 2015 года.
- , с. 43.
- ↑ Курош А. Г. Теория групп. 3-е изд., М.: Наука, 1967.
- А. И. Кострикин. Введение в алгебру, III часть. М.: Физматлит, 2001.
- ↑ Виноградов И. М. . — 5 изд.. — М. — Л. : Гостехиздат, 1952. 18 декабря 2017 года.
- Chris Caldwell, от 22 декабря 2017 на Wayback Machine at glossary.
- ↑ .
- Доказательство . Нечётное число p , не кратное 3, равно 1 или 2 по модулю 3 и равно 1, 3, 5 или 7 по модулю 8. При возведении в квадрат это даёт 1 по модулю 3 и 1 по модулю 8. Вычитая 1, получаем 0 по модулю 3 и 0 по модулю 8. Следовательно, кратно 3 и кратно 8; следовательно, оно кратно 24
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Эти 2 свойства непосредственно следуют из формул разложения суммы и разности степеней
- , с. 332.
- ↑ Graham, Ronald L. (1935- ). . — Moskva: Izdatelʹstvo "Mir", 1998. — 703, [1] s. с. — ISBN 5030017933 .
- Sandifer, Charles Edward, 1951-. . — Washington, D.C.: Mathematical Association of America, 2007. — xix, 391 pages с. — ISBN 0883855593 .
- Bach, Eric. . — Cambridge, Mass.: MIT Press, ©1996-. — volumes <1> с. — ISBN 0262024055 .
- W. R. Alford, Andrew Granville, Carl Pomerance. // Annals of Mathematics. — 1994. — Т. 139 , вып. 3 . — С. 703—722 . — doi : . 26 февраля 2019 года.
- Charles C. Sims. (англ.) // Proceedings of the London Mathematical Society. — 1965-01-01. — Vol. s3—15 , iss. 1 . — P. 151—166 . — ISSN . — doi : . 23 декабря 2017 года.
- Jacobson, Nathan, 1910-1999. . — 2nd ed., Dover ed. — Mineola, N.Y.: Dover Publications, 2009. — 2 volumes с. — ISBN 9780486471877 .
- Сагалович Ю.Л. . — 2011. — 302 с. 25 декабря 2017 года.
- Ferguson, Niels. . — New York: Wiley, 2003. — xx, 410 pages с. — ISBN 0471223573 . 10 июня 2009 года.
- W. Diffie, M. Hellman. // IEEE Transactions on Information Theory. — November 1976. — Т. 22 , вып. 6 . — С. 644—654 . — ISSN . — doi : . 28 декабря 2017 года.
- , p. 175.
- Boneh D. (англ.) // Notices of the American Mathematical Society / — AMS , 1999. — Vol. 46, Iss. 2. — P. 203–213. — ISSN ;
- ↑ RSA Laboratories, {{{2}}}. . Опубликовано 18 мая 2007.
- Jones J. P., Sato D., Wada H., Wiens D. (англ.) // Amer. Math. Mon. : journal. — 1976. — Vol. 83 , no. 6 . — P. 449—464 . 31 марта 2010 года.
- Yuri Matiyasevich, (недоступная ссылка)
- от 6 августа 2010 на Wayback Machine . The Prime Glossary.
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- . Дата обращения: 20 мая 2013. 7 июня 2013 года.
- . Дата обращения: 21 мая 2013. 18 мая 2013 года.
- ↑ . Polymath. Дата обращения: 21 июля 2013. 28 февраля 2020 года.
- (2015). . Annals of Mathematics . 181 (1): 383—413. arXiv : . doi : . MR . S2CID .
-
D.H.J. Polymath (2014). "Variants of the Selberg sieve, and bounded intervals containing many primes".
Research in the Mathematical Sciences
.
1
(12).
arXiv
:
.
doi
:
.
MR
.
S2CID
.
{{ cite journal }}: Википедия:Обслуживание CS1 (не помеченный открытым DOI) ( ссылка ) - Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Обобщение на произвольные полугруппы см. в книге Куроша.
- , с. 75.
- ↑ , с. 82—83.
- , с. 89.
- , с. 77—78.
- William W. Adams, Larry Joel Goldstein (1976), Introduction to Number Theory, p. 250, Prentice-Hall, Inc., ISBN 0-13-491282-9
- ↑ . Дата обращения: 23 декабря 2017. 15 декабря 2020 года.
- Винберг Э. Б. Алгебра многочленов. — М. : Просвещение, 1980. — С. 122—124. — 176 с.
Литература
- Ван дер Варден . Алгебра. Определения, теоремы, формулы. — СПб. : Лань, 2004. — 624 с. — ISBN 5-8114-0552-9 .
- Василенко О. Н. . — М. : МЦНМО , 2003. — 328 с. — ISBN 5-94057-103-4 . от 27 января 2007 на Wayback Machine
- Винберг Э. Б. // Математическое просвещение — М. : Изд-во МЦНМО , 2008. — Т. 12. — С. 43—53.
- Гальперин Г. // Квант . — № 4 . — С. 9—14,38 .
- Генри С. Уоррен, мл. Глава 16. Формулы для простых чисел // Алгоритмические трюки для программистов = Hacker's Delight. — М. : «Вильямс», 2007. — 288 с. — ISBN 0-201-91465-4 .
- Карпушина Н. // Наука и жизнь . — 2010. — № 5 .
- Кордемский Б. А. . — М. : ГИФМЛ, 1958. — 576 с.
- Кормен Т., Лейзер Ч. Глава 33.8. Проверка чисел на простоту // . — М. : МЦНМО, 2002. — С. 765—772. — ISBN 5-900916-37-5 .
- Крэндалл Р. , Померанс К. Простые числа. Криптографические и вычислительные аспекты = Prime Numbers: A Computational Perspective. — М. : УРСС , Либроком, 2011. — 664 с. — ISBN 978-5-397-02060-2 .
- Курош А. Г. Лекции по общей алгебре. — 2-е изд.. — Наука, 1973.
- Ленг С. Алгебра. — М. : Мир, 1967.
- Матиясевич Ю. . // Квант . — 1975. — № 5 . — С. 5—13 .
- Нестеренко Ю. В. // / Под редакцией В. В. Ященко. — Питер, 2001. — 288 с. — ISBN 5-318-00443-1 .
- Цагер Д. // Успехи математических наук . — Российская академия наук , 1984. — Т. 39 , № 6(240) . — С. 175—190 .
- Черёмушкин А. В. . — М. : МЦНМО , 2002. — 104 с. — 2000 экз. — ISBN 5-94057-060-7 . 31 мая 2013 года. .
- Простое число // / Сост. А. П. Савин. — М. : Педагогика , 1985. — С. —263. — 352 с.
- Энрике Грасиан . Простые числа. Долгая дорога к бесконечности. — Де Агостини, 2014. — Т. 3. — 148 с. — (Мир математики). — ISBN 978-5-9774-0682-6 . — ISBN 978-5-9774-0637-6 .
- , (англ.) // — 2012. — Vol. 9, Iss. 1, No 3. — P. 175—178. — ISSN ;
- Crandall R., Pomerance C. Глава 3. «Recognizing Primes and Composites». Глава 4. «Primality Proving» // . — Springer, 2005. — С. 117—224. — ISBN 0-387-25282-7 .
Ссылки
- Кноп К. .
- (англ.) — база данных наибольших известных простых чисел (англ.) .
- (исп.) .
- (англ.) .
- 2021-07-06
- 2























































![{\displaystyle [N,2N]}](/images/009/178/9178346/64.jpg?rand=548401)




























![{\displaystyle P_{n}=[A^{3^{n}}],}](/images/009/178/9178346/93.jpg?rand=297935)














































































![{\displaystyle {\begin{aligned}{\bigl (}k+2{\bigr )}{\bigl \{}1&-{\bigl [}wz+h+j-q{\bigr ]}^{2}-{\bigl [}(gk+2g+k+1)(h+j)+h-z{\bigr ]}^{2}-{\bigl [}2n+p+q+z-e{\bigr ]}^{2}\\&-{\bigl [}16(k+1)^{3}(k+2)(n+1)^{2}+1-f^{2}{\bigr ]}^{2}-{\bigl [}e^{3}(e+2)(a+1)^{2}+1-o^{2}{\bigr ]}^{2}-{\bigl [}(a^{2}-1)y^{2}+1-x^{2}{\bigr ]}^{2}\\&-{\bigl [}16r^{2}y^{4}(a^{2}-1)+1-u^{2}{\bigr ]}^{2}-{\bigl [}((a+u^{2}(u^{2}-a))^{2}-1)(n+4dy)^{2}+1-(x+cu)^{2}{\bigr ]}^{2}-{\bigl [}n+l+v-y{\bigr ]}^{2}\\&-{\bigl [}(a^{2}-1)l^{2}+1-m^{2}{\bigr ]}^{2}-{\bigl [}ai+k+1-l-i{\bigr ]}^{2}-{\bigl [}p+l(a-n-1)+b(2an+2a-n^{2}-2n-2)-m{\bigr ]}^{2}\\&-{\bigl [}q+y(a-p-1)+s(2ap+2a-p^{2}-2p-2)-x{\bigr ]}^{2}-{\bigl [}z+pl(a-p)+t(2ap-p^{2}-1)-pm{\bigr ]}^{2}{\bigr \}}\end{aligned}}}](/images/009/178/9178346/172.jpg?rand=516720)













































![{\displaystyle \mathbb {Z} [\omega ]}](/images/009/178/9178346/219.jpg?rand=709799)










![{\displaystyle K[x]}](/images/009/178/9178346/230.jpg?rand=397438)