Interested Article - Двадцатичетырёхъячейник

- 2021-08-06
- 1
| Двадцатичетырёхъячейник | |
|---|---|
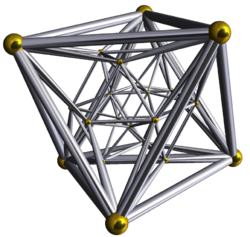
Диаграмма Шлегеля : проекция ( перспектива ) двадцатичетырёхъячейника в трёхмерное пространство |
|
| Тип | Правильный четырёхмерный политоп |
| Символ Шлефли | {3,4,3} |
| Ячеек | 24 |
| Граней | 96 |
| Рёбер | 96 |
| Вершин | 24 |
| Вершинная фигура | Куб |
| Двойственный политоп | Он же ( самодвойственный ) |

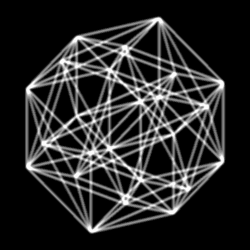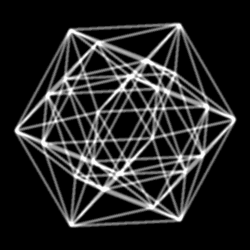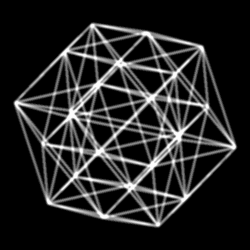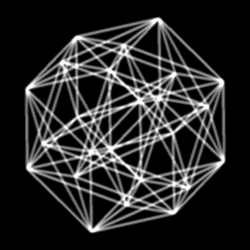

Пра́вильный двадцатичетырёхъяче́йник , или просто двадцатичетырёхъяче́йник , или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из шести правильных многоячейников в четырёхмерном пространстве .
Открыт Людвигом Шлефли в середине 1850-х годов . Символ Шлефли двадцатичетырёхъячейника — {3,4,3}.
Двойственен сам себе; двадцатичетырёхъячейник — единственный самодвойственный правильный политоп размерности больше 2, не являющийся симплексом . Этим обусловлена уникальность двадцатичетырёхъячейника: в отличие от пяти других правильных многоячейников, он не имеет аналога среди платоновых тел .
Описание
Ограничен 24 трёхмерными ячейками — одинаковыми октаэдрами . Угол между двумя смежными ячейками равен в точности
Его 96 двумерных граней — одинаковые правильные треугольники . Каждая грань разделяет 2 примыкающие к ней ячейки.
Имеет 96 рёбер равной длины, расположенных так же, как рёбра трёх тессерактов с общим центром. На каждом ребре сходятся по 3 грани и по 3 ячейки.
Имеет 24 вершины, расположенные так же, как вершины трёх шестнадцатиячейников с общим центром. В каждой вершине сходятся по 8 рёбер, по 12 граней и по 6 ячеек.
Двадцатичетырёхъячейник можно рассматривать как полностью усечённый шестнадцатиячейник.
Двадцатичетырёхъячейник можно собрать из двух равных тессерактов, разрезав один из них на 8 одинаковых кубических пирамид , основания которых — 8 ячеек тессеракта, а вершины совпадают с его центром, и затем приложив эти пирамиды к 8 кубическим ячейкам другого тессеракта. В трёхмерном пространстве аналогичным образом можно из двух равных кубов собрать ромбододекаэдр — который, однако, не является правильным .
В координатах
Первый способ расположения
Двадцатичетырёхъячейник можно разместить в декартовой системе координат так, чтобы 8 из его вершин имели координаты (эти вершины расположены так же, как вершины шестнадцатиячейника ), а остальные 16 вершин — координаты (они расположены так же, как вершины тессеракта ; кроме того, те 8 из них, среди координат которых нечётное число отрицательных, образуют вершины другого шестнадцатиячейника, а прочие 8 — вершины третьего шестнадцатиячейника).
При этом ребром будут соединены те вершины, у которых все четыре координаты различаются на — либо одна из координат различается на а остальные совпадают.
Начало координат будет центром симметрии двадцатичетырёхъячейника, а также центром его вписанной, описанной и полувписанных трёхмерных гиперсфер .
Второй способ расположения
Кроме того, двадцатичетырёхъячейник можно разместить так, чтобы координаты всех его 24 вершин были всевозможными перестановками чисел (эти точки — центры 24 ячеек многоячейника, описанного в предыдущем разделе).
При этом ребром будут соединены те вершины, у которых какие-либо две координаты различаются на а другие две совпадают.
Центром многоячейника снова будет начало координат.
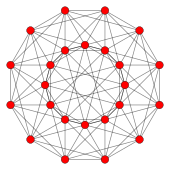
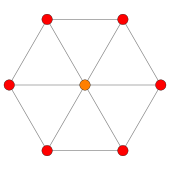
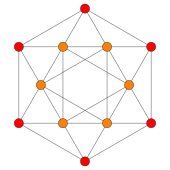
Ортогональные проекции на плоскость
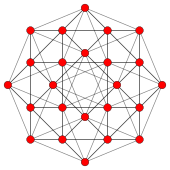
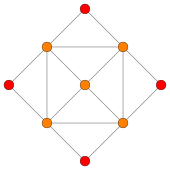
Метрические характеристики
Если двадцатичетырёхъячейник имеет ребро длины то его четырёхмерный гиперобъём и трёхмерная гиперплощадь поверхности выражаются соответственно как
Радиус описанной трёхмерной гиперсферы (проходящей через все вершины многоячейника) при этом будет равен
радиус внешней полувписанной гиперсферы (касающейся всех рёбер в их серединах) —
радиус внутренней полувписанной гиперсферы (касающейся всех граней в их центрах) —
радиус вписанной гиперсферы (касающейся всех ячеек в их центрах) —
Заполнение пространства
Двадцатичетырёхъячейниками можно замостить четырёхмерное пространство без промежутков и наложений.
Примечания
- // Glossary for Hyperspace.
Ссылки
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
| Основные выпуклые правильные и однородные политопы в размерностях 2—10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A n | B n | I₂(p) / D n | E₆ / / E₈ / F₄ / G₂ | |||||||||
| Правильный многоугольник | Правильный треугольник | Квадрат | Правильный p-угольник | Правильный шестиугольник | Правильный пятиугольник | |||||||
| Однородный многогранник | Правильный тетраэдр | Правильный октаэдр • Куб | Полукуб | Правильный додекаэдр • Правильный икосаэдр | ||||||||
| Пятиячейник | 16-ячейник • Тессеракт | Полутессеракт | 24-ячейник | 120-ячейник • 600-ячейник | ||||||||
| Правильный 5-симплекс | 5-ортоплекс • 5-гиперкуб | 5-полугиперкуб | ||||||||||
| Правильный 6-симплекс | 6-ортоплекс • 6-гиперкуб | • | ||||||||||
| Правильный 7-симплекс | • 7-гиперкуб | • • | ||||||||||
| Правильный 8-симплекс | • 8-гиперкуб | • • | ||||||||||
| Правильный 9-симплекс | • 9-гиперкуб | |||||||||||
| Правильный 10-симплекс | • 10-гиперкуб | |||||||||||
| Однородный n - политоп | Правильный n - симплекс | n - ортоплекс • n - гиперкуб | n - полугиперкуб | • • | n - пятиугольный многогранник | |||||||
| Темы: Семейства политопов • Правильные политопы • Список правильных политопов и их соединений | ||||||||||||
- 2021-08-06
- 1




 (эти вершины расположены так же, как вершины
(эти вершины расположены так же, как вершины
 (они расположены так же, как вершины
(они расположены так же, как вершины
 — либо одна из координат различается на
— либо одна из координат различается на
 а остальные совпадают.
а остальные совпадают.
 будет центром симметрии двадцатичетырёхъячейника, а также центром его вписанной, описанной и полувписанных
будет центром симметрии двадцатичетырёхъячейника, а также центром его вписанной, описанной и полувписанных
 (эти точки — центры 24 ячеек многоячейника, описанного в предыдущем разделе).
(эти точки — центры 24 ячеек многоячейника, описанного в предыдущем разделе).
 а другие две совпадают.
а другие две совпадают.
 то его четырёхмерный
то его четырёхмерный





