Interested Article - Плосконосый додекаэдр

Плосконосый додекаэдр


Тип	Полуправильный многогранник
Грань	пятиугольник , треугольник
Граней	$92$ $92$
Рёбер	$150$ $150$
Вершин	$60$ $60$
Граней при вершине	$5$ $5$
Телесный угол	3-3:164°10’31"(164.18°) 3-5=152°55’53"(152.93°)
Символ Шлефли	sr{5,3} или $s{\begin{Bmatrix}5\\3\end{Bmatrix}}$ $s\begin{Bmatrix} 5 \\ 3 \end{Bmatrix}$
	2 3 5
Диаграмма Коксетера
Симметрии вращения	I , [5,3] ⁺ , (532), порядок 60
Двойственный многогранник	Пентагональный гексаконтаэдр
Развёртка
С раскраской граней	Вершинная фигура

Плосконосый додекаэдр , курносый додекаэдр или плосконосый икосододекаэдр — это полуправильный многогранник (архимедово тело), одно из тринадцати выпуклых непризматических тел, гранями которых являются два или более правильных многоугольника .

Плосконосый додекаэдр имеет 92 грани (наибольшее количество из всех архимедовых тел), 12 из них являются пятиугольниками , а остальные 80 — правильными треугольниками . У него 150 рёбер и 60 вершин.

Многогранник имеет две различные формы, являющиеся (или « энантиоморфным видом ») друг друга. Объединение обоих видов образует , а выпуклая оболочка этой конструкции является ромбоусечённым икосододекаэдром .

Кеплер первоначально назвал его в 1619 по латински dodecahedron simum в своей книге Harmonices Mundi . Гарольд Коксетер заметил, что многогранник можно получить равным образом из додекаэдра или икосаэдра и назвал его плосконосым икосододекаэдром , с вертикальным символом Шлефли $s{\begin{Bmatrix}5\\3\end{Bmatrix}}$ $s\begin{Bmatrix} 5 \\ 3 \end{Bmatrix}$ .

Отношение длины ребра "a" к диаметру описанного шара "D":

D=4.311675*a

Декартовы координаты

Декартовыми координатами вершин плосконосого додекаэдра являются все чётные перестановки

(±2α, ±2, ±2β),

(±(α+β/ϕ+ϕ), ±(−αϕ+β+1/ϕ), ±(α/ϕ+βϕ−1)),

(±(α+β/ϕ−ϕ), ±(αϕ−β+1/ϕ), ±(α/ϕ+βϕ+1)),

(±(−α/ϕ+βϕ+1), ±(−α+β/ϕ−ϕ), ±(αϕ+β−1/ϕ)) и

(±(−α/ϕ+βϕ−1), ±(α−β/ϕ−ϕ), ±(αϕ+β+1/ϕ)),

с чётным числом знаков плюс, где

α = ξ − 1 / ξ

и

β = ξϕ + ϕ ² + ϕ /ξ,

Здесь ϕ = (1 + √5)/2 — золотое сечение , а ξ является вещественным решением уравнения ξ ³ − 2ξ = ϕ и это число равно

\xi ={\sqrt[{3}]{{\frac {\phi }{2}}+{\frac {1}{2}}{\sqrt {\phi -{\frac {5}{27}}}}}}+{\sqrt[{3}]{{\frac {\phi }{2}}-{\frac {1}{2}}{\sqrt {\phi -{\frac {5}{27}}}}}}

\xi = \sqrt[3]{\frac{\phi}{2} + \frac{1}{2}\sqrt{\phi - \frac{5}{27}}} + \sqrt[3]{\frac{\phi}{2} - \frac{1}{2}\sqrt{\phi - \frac{5}{27}}}

или, приближённо, 1,7155615.

Этот плосконосый додекаэдр имеет длину ребра примерно 6,0437380841.

Трансформация из ромбоикосидодекаэдра в плосконосый додекаэдр

Если взять нечётные перестановки вышеприведённых координат с чётным числом знаков плюс, получим другую, энантиоморфную форму первого. Хотя это и не сразу очевидно, тело, полученное из чётных перестановок, является тем же самым, что и из нечётных. Тем же образом, зеркальное отображение многогранника будет соответствовать либо чётным перестановкам, либо нечётным.

Площадь поверхности и объём

Длиной ребра 1 площадь поверхности равна

A=20{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\approx 55,28674495844515

A=20{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\approx 55,28674495844515

а объём равен

V={\frac {12\xi ^{2}(3\phi +1)-\xi (36\phi +7)-(53\phi +6)}{6{\sqrt {3-\xi ^{2}}}^{3}}}\approx 37,61664996273336

V={\frac {12\xi ^{2}(3\phi +1)-\xi (36\phi +7)-(53\phi +6)}{6{\sqrt {3-\xi ^{2}}}^{3}}}\approx 37,61664996273336

,

где ϕ — золотое сечение .

Плосконосый додекаэдр имеет наивысшую сферичность из всех архимедовых тел .

Ортогональные проекции

Плосконосый додекаэдр имеет две специальные ортогональные проекции , центрированные относительно двух типов граней — треугольных и пятиугольных, соответствующие плоскостям Коксетера A ₂ и H ₂ .

Ортогональные проекции
Центрирован относительно	Треугольной грани	Пятиугольной грани	Ребра
Изображение
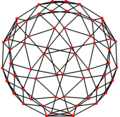
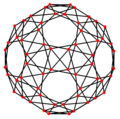
Проективная симметрия	[3]	[5] ⁺	[2]
Двойственный многогранник

Геометрические связи

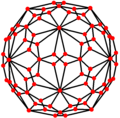
Вращение курносого додекаэдра
Вращение по спирали вправо Вращение по спирали влево

Плосконосый додекаэдр может быть получен из двенадцати правильных пятиугольных граней додекаэдра путём их вытягивания наружу , так что они перестают касаться друг друга. При вытягивании на подходящее расстояние это даст ромбоикосидодекаэдр , если заполнить полученное пространство между разделёнными рёбрами квадратами, а между разделёнными вершинами — треугольниками. Но чтобы получить плосконосый вид, заполняем только треугольные грани, квадратные промежутки оставляем пустыми. Теперь поворачиваем пятиугольники относительно их центров вместе с треугольниками, пока квадратные промежутки не превратятся в равносторонние треугольники.

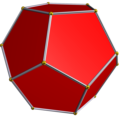
Додекаэдр	Ромбоикосидодекаэдр ( Расширенный додекаэдр )	Плосконосый додекаэдр

Плосконосый додекаэдр можно также получить из ромбоусечённого икосододекаэдра путём . Шестьдесят вершин ромбоусечённого икосододекаэдра образуют многогранник, топологически эквивалентный одному плосконосому додекаэдру. Оставшиеся шестьдесят образуют его зеркальное отражение. Получившийся многогранник вершинно транзитивен , но не однороден, поскольку имеет рёбра разной длины, необходима некоторая деформация, чтобы привести его к однородному многограннику.

Связанные многогранники и мозаики

Семейство однородных икосаэдральных многогранников
Симметрия : [5,3] , (*532)							[5,3] ⁺ , (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}
Двойственные к однородным многогранникам

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Этот полуправильный многогранник принадлежит последовательности многогранников и мозаик с вершинной фигурой (3.3.3.3. n ) и диаграммой Коксетера — Дынкина . Эти фигуры и их двойственные имеют (n32) вращательную и существуют в евклидовой плоскости для n=6 и гиперболической плоскости для любого n, большего 6. Можно считать, что последовательность начинается с n=2, если допустить, что некоторое множество граней вырождается в двуугольники .

n 32 симметрии плосконосых мозаик: *3.3.3.3.n*
Симметрия	Сферическая				Евклидоваn	Компактная гиперболич.		Паракомп.
Симметрия	232	332	432	532	632	732	832	∞32
Плосконосые фигуры
Конфигурация	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4		3.3.3.3.6		3.3.3.3.8
Фигуры
Конфигурация	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Граф плосконосого додекаэдра

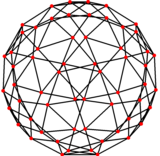
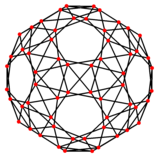
В теории графов граф плосконосого додекаэдра — это плосконосого додекаэдра. Он имеет 60 вершин и 150 рёбер и является архимедовым графом .

Ортогональные проекции

См. также

Преобразование плоского многоугольника в многогранник Анимация
ccw и cw — вращающиеся плосконосые додекаэдры

Примечания

, с. 437, 435.
, с. 183.
, с. 20, 42.
, с. 269.

Литература

М. Веннинджер . Модели многогранников. — Мир , 1974.
Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова , А. И. Маркушевича , А. Я. Хинчина . — М. : Государственное издательство физико-математической литературы , 1963. — С. 382-447.
Л. А. Люстерник . Выпуклые фигуры и многогранники. — М. : Государственное издательство технико-теоретической литературы , 1956.
Udaya Jayatilake. Calculations on face and vertex regular polyhedra // Mathematical Gazette. — 2005. — Т. 89 , вып. 514 (March) . — С. 76–81 .
Robert Williams. . — Dover Publications, Inc., 1979. — ISBN 0-486-23729-X .. (Секция 3-9)
P. Cromwell. Polyhedra. — United Kingdom: Cambridge, 1997. — С. 79–86 Archimedean solids . — ISBN 0-521-55432-2 .
R.C. Read, R.J. Wilson. An Atlas of Graphs. — Oxford University Press, 1998.