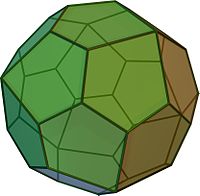
Дельтоида́льный икоситетра́эдр (от « дельтоид » и др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре», ἕδρα — «грань»), также называемый тетрагонтриокта́эдром (от др.-греч. τέτταρες — «четыре», γωνία — «угол», τρία — «три», οκτώ — «восемь» и ἕδρα — «грань»), — полуправильный многогранник (каталаново тело), двойственный ромбокубооктаэдру .

Составлен из 24 одинаковых выпуклых дельтоидов .

Имеет 26 вершин. В 8 вершинах (расположенных так же, как вершины куба ) сходятся по 3 грани своими тупыми углами; в 6 вершинах (расположенных так же, как вершины октаэдра ) сходятся по 4 грани острыми углами, противоположными тупому; в остальных 12 вершинах (расположенных так же, как вершины кубооктаэдра ) сходятся по 4 грани острыми углами, соседними с тупым.

• 
  8 вершин расположены так же, как вершины куба
• 
  6 вершин расположены так же, как вершины октаэдра
• 
  12 вершин расположены так же, как вершины кубооктаэдра

Имеет 48 рёбер — 24 «длинных» (вместе образующих нечто вроде «раздутого» остова октаэдра) и 24 «коротких» (образующих «раздутый» остов куба).

Дельтоидальный икоситетраэдр — одно из шести каталановых тел, в которых нет гамильтонова цикла ; гамильтонова пути для всех шести также нет.

Метрические характеристики и углы

Если «короткие» рёбра дельтоидального икоситетраэдра имеют длину ${\displaystyle b}$ , то его «длинные» рёбра имеют длину

${\displaystyle a={\frac {1}{2}}\left(4-{\sqrt {2}}\right)b\approx 1{,}2928932b.}$

Площадь поверхности и объём многогранника при этом выражаются как

${\displaystyle S=6{\sqrt {29-2{\sqrt {2}}}}\;b^{2}\approx 30{,}6948957b^{2},}$

${\displaystyle V={\sqrt {122+71{\sqrt {2}}}}\;b^{3}\approx 14{,}9133887b^{3}.}$

Радиус вписанной сферы (касающейся всех граней многогранника в их центрах вписанных окружностей ) при этом будет равен

${\displaystyle r={\frac {1}{2}}{\sqrt {{\frac {1}{17}}\left(78+47{\sqrt {2}}\right)}}\;b\approx 1{,}4575767b,}$

радиус полувписанной сферы (касающейся всех рёбер) —

${\displaystyle \rho ={\frac {1}{4}}\left(2+3{\sqrt {2}}\right)b\approx 1{,}5606602b,}$

радиус окружности, вписанной в грань —

${\displaystyle r_{\Gamma \mathrm {P} }={\sqrt {\rho ^{2}-r^{2}}}={\frac {1}{2}}{\sqrt {{\frac {1}{34}}\left(31+8{\sqrt {2}}\right)}}\;b\approx 0{,}5577905b,}$

бо́льшая диагональ грани (делящая грань на два равнобедренных треугольника ) —

${\displaystyle e={\frac {1}{2}}{\sqrt {10+{\sqrt {2}}}}\;b\approx 1{,}6892464b,}$

меньшая диагональ грани (делящая грань на два равных треугольника) —

${\displaystyle f={\frac {1}{2}}{\sqrt {12-2{\sqrt {2}}}}\;b\approx 1{,}5142302b.}$

Описать около дельтоидального икоситетраэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

Тупой угол грани (между двумя «короткими» сторонами) равен ${\displaystyle \arccos \left(-{\frac {2+{\sqrt {2}}}{8}}\right)\approx 115{,}26^{\circ };}$ три острых угла грани равны ${\displaystyle \arccos \,{\frac {2-{\sqrt {2}}}{4}}\approx 81{,}58^{\circ }.}$

Двугранный угол при любом ребре одинаков и равен ${\displaystyle \arccos \left(-{\frac {7+4{\sqrt {2}}}{17}}\right)\approx 138{,}12^{\circ }.}$

В природе и культуре

В форме дельтоидального икоситетраэдра встречаются кристаллы анальцима , лейцита , спессартина , андрадита , иногда — граната .

• 
  Анальцим
• 
  Лейцит
• 
  Спессартин

Дельтоидальный икоситетраэдр играет важную роль в рассказе Говарда Лавкрафта « Обитающий во Тьме », где фигурирует под принятым в кристаллографии названием «trapezohedron». В стереометрии словом « трапецоэдр » обозначается другой многогранник.

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .