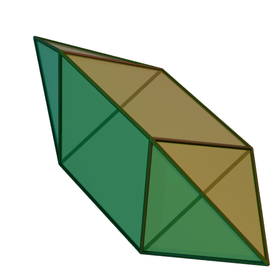
Удлинённая четырёхуго́льная бипирами́да — один из многогранников Джонсона ( J ₁₅ , по Залгаллеру — М ₂ +П ₄ +М ₂ ).

Составлена из 12 граней: 8 правильных треугольников и 4 квадратов . Каждая квадратная грань окружена двумя квадратными и двумя треугольными; каждая треугольная — одной квадратной и двумя треугольными.

Имеет 20 рёбер одинаковой длины. 4 ребра располагаются между двумя квадратными гранями, 8 рёбер — между квадратной и треугольной, остальные 8 — между двумя треугольными.

У удлинённой четырёхугольной бипирамиды 10 вершин. В 8 вершинах (расположенных как вершины куба ) сходятся две квадратных грани и две треугольных; в остальных 2 — четыре треугольных.

Удлинённую четырёхугольную бипирамиду можно получить из трёх многогранников — куба и двух квадратных пирамид , все рёбра у которых одинаковой длины ( J ₁ ), — приложив основания пирамид к двум противоположным граням куба.

Метрические характеристики

Если удлинённая четырёхугольная бипирамида имеет ребро длины ${\displaystyle a}$ , её площадь поверхности и объём выражаются как

${\displaystyle S=\left(4+2{\sqrt {3}}\right)a^{2}\approx 7{,}4641016a^{2},}$

${\displaystyle V=\left(1+{\frac {\sqrt {2}}{3}}\right)a^{3}\approx 1{,}4714045a^{3}.}$

В координатах

Удлинённую четырёхугольную бипирамиду с длиной ребра ${\displaystyle 2}$ можно расположить в декартовой системе координат так, чтобы её вершины имели координаты

• ${\displaystyle (\pm 1;\;\pm 1;\;\pm 1),}$
• ${\displaystyle \left(0;\;0;\;\pm \left(1+{\sqrt {2}}\right)\right).}$

При этом центр симметрии многогранника будет совпадать с началом координат, три из пяти осей симметрии — с осями Ox, Oy и Oz, а три из пяти плоскостей симметрии — с плоскостями xOy, xOz и yOz.

Заполнение пространства

Замостить трёхмерное пространство без промежутков и наложений при помощи многогранников Джонсона J ₁₅ нельзя. Если, однако, немного деформировать удлинённую четырёхугольную бипирамиду, превратив равносторонние треугольники в равнобедренные с отношением сторон ${\displaystyle 2:{\sqrt {3}}:{\sqrt {3}},}$ получим многогранник, изоморфный J ₁₅ , для которого заполнение пространства становится возможным:

На иллюстрации копии многогранника окрашены в три разных цвета в соответствии с их различной ориентацией в пространстве.

В природе и культуре

В форме удлинённой четырёхугольной бипирамиды и близких к ней многогранников встречаются кристаллы циркона :

• 
• 
• 
  Под электронным микроскопом

На гравюре Маурица Эшера (1948) присутствует (у середины верхнего края) многогранник, изоморфный J ₁₅ — несколько «сжатый» так, что вместо квадратных граней у него прямоугольники .

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .