Систе́ма координа́т — комплекс определений, реализующий метод координат , то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа .

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой , а другая — абсциссой . В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами , где начало координат находится в центре сферы.

В географии координаты выбираются как ( приближённо ) сферическая система координат — широта , долгота и высота над известным общим уровнем (например, океана). См. Географические координаты .

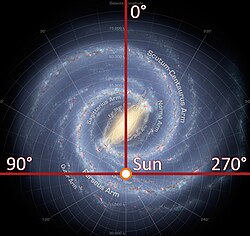
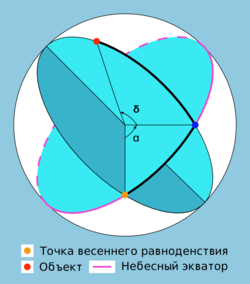
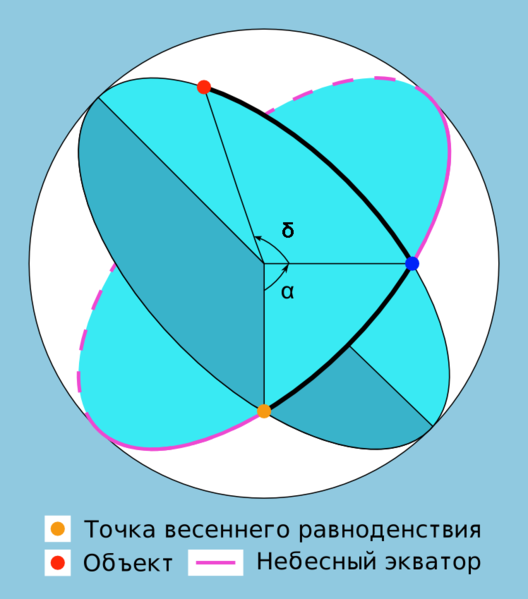
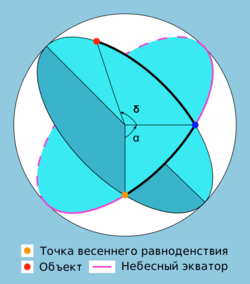
В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение ), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат ).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции .

Основные системы

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты

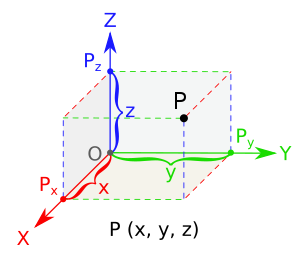
Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел ${\displaystyle (x,y):}$

• ${\displaystyle x}$ — расстояние от точки P до оси y с учетом знака
• ${\displaystyle y}$ — расстояние от точки P до оси x с учетом знака

В пространстве необходимы уже три координаты ${\displaystyle (x,y,z):}$

• ${\displaystyle x}$ — расстояние от точки P до плоскости yz
• ${\displaystyle y}$ — расстояние от точки P до плоскости xz
• ${\displaystyle z}$ — расстояние от точки P до плоскости xy

Полярные координаты

В полярной системе координат , применяемой на плоскости, положение точки P определяется её расстоянием до начала координат r = |OP| и углом φ её радиус-вектора к оси Ox .

В пространстве применяются обобщения полярных координат — цилиндрические и сферические системы координат.

Цилиндрические координаты

Цилиндрические координаты — трёхмерный аналог полярных, в котором точка P представляется упорядоченной тройкой ${\displaystyle (r,\varphi ,z).}$ В терминах декартовой системы координат,

• ${\displaystyle 0\leqslant {r}}$ ( радиус ) — расстояние от оси z до точки P ,
• ${\displaystyle 0\leqslant \varphi <360^{\circ }}$ ( азимут или долгота) — угол между положительной («плюсовой») частью оси x и отрезком, проведённым от полюса до точки P и спроектированной на плоскость xy .
• ${\displaystyle z}$ (высота) равна декартовой z -координате точки P .

Примечание: в литературе для первой (радиальной) координаты иногда используется обозначение ρ , для второй (угловой, или азимутальной) — обозначение θ , для третьей координаты — обозначение h .

Полярные координаты имеют один недостаток: значение φ не определено при r = 0 .

Цилиндрические координаты полезны для изучения систем, симметричных относительно некоторой оси. Например, длинный цилиндр с радиусом R в декартовых координатах (с осью z , совпадающей с осью цилиндра) имеет уравнение ${\displaystyle x^{2}+y^{2}=R^{2},}$ тогда как в цилиндрических координатах оно выглядит гораздо проще, как r = R .

Сферические координаты

Сферические координаты — трёхмерный аналог полярных.

В сферической системе координат расположение точки P определяется тремя компонентами: ${\displaystyle (\rho ,\varphi ,\theta).}$ В терминах декартовой системы координат,

• ${\displaystyle 0\leqslant \rho }$ (радиус) — расстояние от точки P до полюса,
• ${\displaystyle 0\leqslant \varphi \leqslant 360^{\circ }}$ (азимут или долгота) — угол между положительной («плюсовой») полуосью x и проекцией отрезка, проведённого из полюса до точки P , на плоскость xy .
• ${\displaystyle 0\leqslant \theta \leqslant 180^{\circ }}$ (широта или полярный угол) — угол между положительной («плюсовой») полуосью z и отрезком, проведённым из полюса до точки P .

Примечание: в литературе иногда азимут обозначается θ , а полярный угол - φ . Иногда для радиальной координаты используется r вместо ρ . Кроме того, диапазон углов для азимута может выбираться как (−180°, +180°] вместо диапазона [0°, +360°). Наконец, полярный угол может отсчитываться не от положительного направления оси z , а от плоскости xy ; в этом случае он лежит в диапазоне [−90°, +90°], а не в диапазоне [0°, 180°]. Иногда порядок координат в тройке выбирается отличным от описанного; например, полярный и азимутальный углы могут быть переставлены.

Сферическая система координат также имеет недостаток: φ и θ не определены, если ρ = 0; угол φ не определён также и для граничных значений θ = 0 и θ = 180° (или для θ = ±90°, в случае принятия соответствующего диапазона для этого угла).

Для построения точки P по её сферическим координатам нужно от полюса вдоль положительной полуоси z отложить отрезок, равный ρ , повернуть его на угол θ вокруг оси y в направлении положительной полуоси x , и затем повернуть на угол θ вокруг оси z в направлении положительной полуоси y .

Сферические координаты полезны при изучении систем, симметричных относительно точки. Так, уравнение сферы с радиусом R в декартовых координатах с началом отсчёта в центре сферы выглядит как ${\displaystyle x^{2}+y^{2}+z^{2}=R^{2},}$ тогда как в сферических координатах оно становится намного проще: ${\displaystyle \rho =R.}$

Другие распространённые системы координат

• Аффинная (косоугольная) система координат — прямолинейная система координат в аффинном пространстве . На плоскости задается точкой начала координат О и двумя упорядоченными не коллинеарными векторами , которые представляют собой базис. Осями координат в данном случае называются прямые , проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве , соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса .

• Барицентрические координаты были впервые введены в 1827 году А. Мебиусом , решавшим вопрос о центре тяжести масс, расположенных на вершинах треугольника . Они аффинно инвариантны, представляют собой частный случай общих однородных координат . Точка с барицентрическими координатами расположена в n -мерном векторном пространстве E ⁿ , а собственно координаты при этом относятся к фиксированной системе точек, которые не лежат в ( n −1)-мерном подпространстве. Барицентрические координаты используются также и в алгебраической топологии применительно к точкам симплекса .

• Биангулярные координаты — частный случай бицентрических координат, система координат на плоскости, задаваемая двумя фиксированными точками С ₁ и С ₂ , через которые проводится прямая, выступающая в качестве оси абсцисс. Позиция некоторой точки P , которая не лежит на этой прямой, определяется углами PC ₁ C ₂ и PC ₂ C ₁ .

• Биполярные координаты характеризуются тем, что в качестве координатных линий на плоскости в этом случае выступают два семейства окружностей с полюсами A и B , а также семейство окружностей, ортогональных к ним. Преобразование биполярных координат в декартовы прямоугольные осуществляется посредством специальных формул. Биполярные координаты в пространстве называются бисферическими; в этом случае координатными поверхностями являются сферы , поверхности, образуемые вращением дуг окружностей, а также полуплоскости , проходящие через ось O _z .

• Бицентрические координаты — всякая система координат, которая основана на двух фиксированных точках и в рамках которой положение некоторой другой точки определяется, как правило, степенью её удаления или вообще позицией относительно этих двух основных точек. Системы подобного рода могут быть довольно полезны в определённых сферах научных исследований .

• — система координат, которая образуется в том случае, если система биполярных координат на плоскости O _xy параллельно переносится вдоль оси O _z . В качестве координатных поверхностей в этом случае выступают семейство пар круговых цилиндров , оси которых параллельны, семейство ортогональных к ним круговых цилиндров, а также плоскость. Для перевода бицилиндрических координат в декартовы прямоугольные для трехмерного пространства также применяются специальные формулы .

• Диполярные координаты — трехмерная криволинейная ортогональная система координат, основанная на точечном (центральном) диполе, точнее, на его инвариантах преобразования координат. Одним из инвариантов является эквипотенциальная поверхность , которая служит координатной поверхностью; другой инвариант — силовые линии векторного поля , перпендикулярные эквипотенциальным поверхностям. Преобразование сферических или декартовых координат в диполярные осуществляется посредством специальных формул.

• Конические координаты — трехмерная ортогональная система координат, состоящая из концентрических сфер, которые описываются посредством их радиуса , и двух семейств перпендикулярных конусов , расположенных вдоль осей x и z .

• Координаты Риндлера используются преимущественно в рамках теории относительности и описывают ту часть плоского пространства-времени , которая обыкновенно называется пространством Минковского . В специальной теории относительности равномерно ускоряющаяся частица находится в гиперболическом движении , и для каждой такой частицы в координатах Риндлера может быть выбрана такая точка отсчёта , относительно которой она покоится.

• Параболические координаты — это двумерная ортогональная система координат, в которой координатными линиями является совокупность конфокальных парабол . Трехмерная модификация параболических координат строится путём вращения двумерной системы вокруг оси симметрии этих парабол. У параболических координат также имеется определенный спектр потенциальных практических приложений: в частности, они могут использоваться применительно к эффекту Штарка . Параболические координаты связаны определенным отношением с прямоугольными декартовыми .

• Проективные координаты существуют, согласно наименованию, в проективном пространстве П _n ( К ) и представляют собой взаимно однозначное соответствие между его элементами и классами конечных подмножеств элементов тела К , характеризующихся свойствами эквивалентности и упорядоченности. Для определения проективных координат проективных подпространств достаточно определить соответствующие координаты точек проективного пространства. В общем случае относительно некоторого базиса проективные координаты вводятся чисто проективными средствами .

• Тороидальная система координат — трехмерная ортогональная система координат, получаемая в результате вращения двумерной биполярной системы координат вокруг оси, разделяющей два её фокуса. Фокусы биполярной системы, соответственно, превращаются в кольцо с радиусом а , лежащее на плоскости xy тороидальной системы координат, в то время как ось z становится осью вращения системы. Фокальное кольцо также называют иногда базовой окружностью .

• Трилинейные координаты являются одним из образцов однородных координат и имеют своей основой заданный треугольник, так что положение некоторой точки определяется относительно сторон этого треугольника — главным образом степенью удаленности от них, хотя возможны и другие вариации. Трилинейные координаты могут быть относительно просто преобразованы в барицентрические; кроме того, они также конвертируемы в двумерные прямоугольные координаты, для чего используются соответствующие формулы .

• Цилиндрические параболические координаты — трехмерная ортогональная система координат, получаемая в результате пространственного преобразования двумерной параболической системы координат. Координатными поверхностями, соответственно, служат конфокальные параболические цилиндры. Цилиндрические параболические координаты связаны определенным отношением с прямоугольными, могут быть применены в ряде сфер научных исследований .

• Эллипсоидальные координаты — эллиптические координаты в пространстве. Координатными поверхностями в данном случае являются эллипсоиды , однополостные гиперболоиды , а также двуполостные гиперболоиды, центры которых расположены в начале координат. Система ортогональна. Каждой тройке чисел, являющихся эллипсоидальными координатами, соответствуют восемь точек, которые относительно плоскостей системы O _xyz симметричны друг другу .

Переход из одной системы координат в другую

См. также: Преобразование координат

Декартовы и полярные

${\displaystyle x=r\,\cos \varphi ,}$

${\displaystyle y=r\,\sin \varphi ,}$

${\displaystyle r={\sqrt {x^{2}+y^{2}}},}$

${\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}$

где u ₀ — функция Хевисайда с ${\displaystyle u_{0}(0)=0,}$ а sgn — функция signum . Здесь функции u ₀ и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию ( y , x ), которая возвращает правильный φ в необходимом квадранте , определённом координатами x и y .

Декартовы и цилиндрические

${\displaystyle x=r\,\cos \varphi ,}$

${\displaystyle y=r\,\sin \varphi ,}$

${\displaystyle z=z.\quad }$

${\displaystyle r={\sqrt {x^{2}+y^{2}}},}$

${\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}$

${\displaystyle z=z.\quad }$

${\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}r\cos \varphi &-r\sin \varphi &0\\r\sin \varphi &r\cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}},}$

${\displaystyle {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{\sqrt {x^{2}+y^{2}}}}&{\frac {x}{\sqrt {x^{2}+y^{2}}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}$

Декартовы и сферические

${\displaystyle {x}=\rho \,\sin \theta \,\cos \varphi ,\quad }$

${\displaystyle {y}=\rho \,\sin \theta \,\sin \varphi ,\quad }$

${\displaystyle {z}=\rho \,\cos \theta ;\quad }$

${\displaystyle {\rho }={\sqrt {x^{2}+y^{2}+z^{2}}},}$

${\displaystyle {\theta }=\arccos {\frac {z}{\rho }}=\operatorname {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}},}$

${\displaystyle {\varphi }=\operatorname {arctg} {\frac {y}{x}}+\pi \,u_{0}(-x)\,\operatorname {sgn} y.}$

${\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}\sin \theta \cos \varphi &\rho \cos \theta \cos \varphi &-\rho \sin \theta \sin \varphi \\\sin \theta \sin \varphi &\rho \cos \theta \sin \varphi &\rho \sin \theta \cos \varphi \\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}$

${\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}x/\rho &y/\rho &z/\rho \\{\frac {xz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}$

Цилиндрические и сферические

${\displaystyle {r}=\rho \,\sin \theta ,}$

${\displaystyle {\varphi }=\varphi ,\quad }$

${\displaystyle {z}=\rho \,\cos \theta ;}$

${\displaystyle {\rho }={\sqrt {r^{2}+z^{2}}},}$

${\displaystyle {\theta }=\operatorname {arctg} {\frac {z}{r}}+\pi \,u_{0}(-r)\,\operatorname {sgn} z,}$

${\displaystyle {\varphi }=\varphi .\quad }$

${\displaystyle {\begin{pmatrix}dr\\d\varphi \\dh\end{pmatrix}}={\begin{pmatrix}\sin \theta &\rho \cos \theta &0\\0&0&1\\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}$

${\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}{\frac {r}{\sqrt {r^{2}+z^{2}}}}&0&{\frac {z}{\sqrt {r^{2}+z^{2}}}}\\{\frac {-z}{r^{2}+z^{2}}}&0&{\frac {r}{r^{2}+z^{2}}}\\0&1&0\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}.}$

Географическая система координат

Географическая система координат обеспечивает возможность идентификации любой точки на поверхности земного шара совокупностью цифробуквенных обозначений. Как правило, координаты назначаются таким образом, что один из указателей обозначает позицию по вертикали , а другой или совокупность других — по горизонтали . Традиционный набор географических координат — широта , долгота и высота . Географическая система координат с использованием трёх перечисленных указателей является ортогональной.

Широта точки на поверхности Земли определяется как угол между плоскостью экватора и прямой, проходящей через эту точку в виде нормали к поверхности базового эллипсоида, примерно совпадающего по форме с Землёй. Эта прямая обычно проходит в нескольких километрах от центра Земли, за исключением двух случаев: полюсов и экватора (в этих случаях она проходит непосредственно через центр). Линии, соединяющие точки одной широты, именуются параллелями . 0° широты соответствуют плоскости экватора, Северный полюс Земли соответствует 90° северной широты, Южный — соответственно, 90° южной широты. В свою очередь, долгота точки на поверхности Земли определяется как угол в восточном или западном направлении от основного меридиана к другому меридиану, проходящему через эту точку. Меридианы, соединяющие точки одной долготы, представляют собой полуэллипсы, сходящиеся на полюсах. Нулевым считается меридиан, проходящий через королевскую обсерваторию в Гринвиче , близ Лондона . Что касается высоты, то она отсчитывается от условной поверхности геоида , являющегося абстрактным пространственным представлением земного шара.

См. также

Примечания

Литература

• Гельфанд И. М. , Глаголева Е. Г., Кириллов А. А. Издание седьмое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: МЦНМО, 2009.
• Делоне Н. Б. // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб. , 1890—1907.

Ссылки