Interested Article - Замечательные пределы

Замеча́тельные преде́лы — термины, использующиеся в советских и российских учебниках по математическому анализу для обозначения двух широко известных математических тождеств со взятием предела :

Первый замечательный предел:

$\lim _{x\to 0}{\frac {\sin x}{x}}=1.$ $\lim _{{x\to 0}}{\frac {\sin x}{x}}=1.$
Второй замечательный предел:

$\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e.$ $\lim _{{x\to \infty }}\left(1+{\frac {1}{x}}\right)^{x}=e.$

Первый замечательный предел

$\lim _{x\to 0}{\frac {\sin x}{x}}=1$ $\lim _{{x\to 0}}{\frac {\sin x}{x}}=1$

Доказательство:

Рассмотрим односторонние пределы $\lim _{x\to +0}{\frac {\sin x}{x}}$ $\lim _{x\to +0}{\frac {\sin x}{x}}$ и $\lim _{x\to {\displaystyle -}0}{\frac {\sin x}{x}}$ $\lim _{x\to {\displaystyle -}0}{\frac {\sin x}{x}}$ и докажем, что они равны 1.

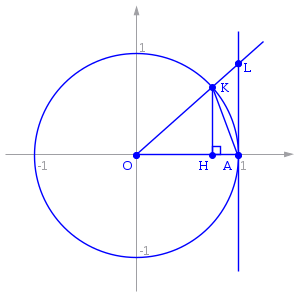
Рассмотрим случай $x\in \left(0;{\frac {\pi }{2}}\right)$ $x\in \left(0;{\frac {\pi }{2}}\right)$ . Отложим этот угол на единичной окружности так, чтобы его вершина совпадала с началом координат, а одна сторона совпадала с осью $OX$ $OX$ . Пусть $K$ $K$ — точка пересечения второй стороны угла с единичной окружностью, а точка $L$ $L$ — с касательной к этой окружности в точке $A=\left(1;0\right)$ $A=\left(1;0\right)$ . Точка $H$ $H$ — проекция точки $K$ $K$ на ось $OX$ $OX$ .

Очевидно, что:

S_{\triangle OKA}<S_{sectKOA}<S_{\triangle OAL}

S_{\triangle OKA}<S_{sectKOA}<S_{\triangle OAL}

(1)

(где $S_{sectKOA}$ $S_{sectKOA}$ — площадь сектора $KOA$ $KOA$ )

Поскольку $\left|KH\right|=\sin x,\,\left|LA\right|=\operatorname {tg} x$ $\left|KH\right|=\sin x,\,\left|LA\right|=\operatorname {tg} x$ :

S_{\triangle OKA}={\frac {1}{2}}\cdot \left|OA\right|\cdot \left|KH\right|={\frac {1}{2}}\cdot 1\cdot \sin x={\frac {\sin x}{2}}

S_{\triangle OKA}={\frac {1}{2}}\cdot \left|OA\right|\cdot \left|KH\right|={\frac {1}{2}}\cdot 1\cdot \sin x={\frac {\sin x}{2}}

S_{sectKOA}={\frac {1}{2}}\cdot \left|OA\right|^{2}\cdot x={\frac {x}{2}}

S_{sectKOA}={\frac {1}{2}}\cdot \left|OA\right|^{2}\cdot x={\frac {x}{2}}

S_{\triangle OAL}={\frac {1}{2}}\cdot \left|OA\right|\cdot \left|LA\right|={\frac {\operatorname {tg} x}{2}}

S_{\triangle OAL}={\frac {1}{2}}\cdot \left|OA\right|\cdot \left|LA\right|={\frac {\operatorname {tg} x}{2}}

Подставляя в (1), получим:

{\frac {\sin x}{2}}<{\frac {x}{2}}<{\frac {\operatorname {tg} x}{2}}

{\frac {\sin x}{2}}<{\frac {x}{2}}<{\frac {\operatorname {tg} x}{2}}

Так как при $x\to +0:\sin x>0,\,x>0,\,\operatorname {tg} x>0$ $x\to +0:\sin x>0,\,x>0,\,\operatorname {tg} x>0$ :

{\frac {1}{\operatorname {tg} x}}<{\frac {1}{x}}<{\frac {1}{\sin x}}

{\frac {1}{\operatorname {tg} x}}<{\frac {1}{x}}<{\frac {1}{\sin x}}

Умножаем на $\sin x$ $\sin x$ :

\cos x<{\frac {\sin x}{x}}<1

\cos x<{\frac {\sin x}{x}}<1

Перейдём к пределу:

\lim _{x\to +0}\cos x\leqslant \lim _{x\to +0}{\frac {\sin x}{x}}\leqslant 1

\lim _{x\to +0}\cos x\leqslant \lim _{x\to +0}{\frac {\sin x}{x}}\leqslant 1

1\leqslant \lim _{x\to +0}{\frac {\sin x}{x}}\leqslant 1

1\leqslant \lim _{x\to +0}{\frac {\sin x}{x}}\leqslant 1

\lim _{x\to +0}{\frac {\sin x}{x}}=1

\lim _{x\to +0}{\frac {\sin x}{x}}=1

Найдём левый односторонний предел (так как функция четна, в этом нет необходимости, достаточно доказать это для правого предела):

\lim _{x\to -0}{\frac {\sin x}{x}}=\left[{\begin{matrix}u=-x\\x=-u\\u\to +0\\x\to -0\end{matrix}}\right]=\lim _{u\to +0}{\frac {\sin(-u)}{-u}}=\lim _{u\to +0}{\frac {-\sin(u)}{-u}}=\lim _{u\to +0}{\frac {\sin(u)}{u}}=1

\lim _{x\to -0}{\frac {\sin x}{x}}=\left[{\begin{matrix}u=-x\\x=-u\\u\to +0\\x\to -0\end{matrix}}\right]=\lim _{u\to +0}{\frac {\sin(-u)}{-u}}=\lim _{u\to +0}{\frac {-\sin(u)}{-u}}=\lim _{u\to +0}{\frac {\sin(u)}{u}}=1

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия:

$\lim _{x\to 0}{\frac {\operatorname {tg} x}{x}}=1$ $\lim _{x\to 0}{\frac {\operatorname {tg} x}{x}}=1$
$\lim _{x\to 0}{\frac {\operatorname {arcsin} x}{x}}=1$ $\lim _{x\to 0}{\frac {\operatorname {arcsin} x}{x}}=1$
$\lim _{x\to 0}{\frac {\operatorname {arctg} x}{x}}=1$ $\lim _{x\to 0}{\frac {\operatorname {arctg} x}{x}}=1$
$\lim _{x\to 0}{\frac {1-\cos x}{\frac {x^{2}}{2}}}=1$ $\lim _{{x\to 0}}{\frac {1-\cos x}{{\frac {x^{2}}{2}}}}=1$

Доказательство следствий

\lim _{x\to 0}{\frac {\operatorname {tg} x}{x}}=\lim _{x\to 0}{\frac {\sin x}{x\cos x}}=\lim _{x\to 0}{\frac {\sin x}{x}}\cdot \lim _{x\to 0}{\frac {1}{\cos x}}=1\cdot 1=1

\lim _{x\to 0}{\frac {\operatorname {tg} x}{x}}=\lim _{x\to 0}{\frac {\sin x}{x\cos x}}=\lim _{x\to 0}{\frac {\sin x}{x}}\cdot \lim _{x\to 0}{\frac {1}{\cos x}}=1\cdot 1=1

\lim _{x\to 0}{\frac {\operatorname {arcsin} x}{x}}=\left[{\begin{matrix}u=\operatorname {arcsin} x\\x=\sin u\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {u}{\sin u}}=1

\lim _{x\to 0}{\frac {\operatorname {arcsin} x}{x}}=\left[{\begin{matrix}u=\operatorname {arcsin} x\\x=\sin u\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {u}{\sin u}}=1

\lim _{x\to 0}{\frac {\operatorname {arctg} x}{x}}=\left[{\begin{matrix}u=\operatorname {arctg} x\\x=\operatorname {tg} u\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {u}{\operatorname {tg} u}}=1

\lim _{x\to 0}{\frac {\operatorname {arctg} x}{x}}=\left[{\begin{matrix}u=\operatorname {arctg} x\\x=\operatorname {tg} u\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {u}{\operatorname {tg} u}}=1

\lim _{x\to 0}{\frac {1-\cos x}{\frac {x^{2}}{2}}}=\lim _{x\to 0}{\frac {2\cdot \sin ^{2}{\frac {x}{2}}}{2\cdot \left({\frac {x}{2}}\right)^{2}}}=\lim _{{\frac {x}{2}}\to 0}\left({\frac {\sin {\frac {x}{2}}}{\frac {x}{2}}}\right)^{2}=1^{2}=1

\lim _{x\to 0}{\frac {1-\cos x}{\frac {x^{2}}{2}}}=\lim _{x\to 0}{\frac {2\cdot \sin ^{2}{\frac {x}{2}}}{2\cdot \left({\frac {x}{2}}\right)^{2}}}=\lim _{{\frac {x}{2}}\to 0}\left({\frac {\sin {\frac {x}{2}}}{\frac {x}{2}}}\right)^{2}=1^{2}=1

Второй замечательный предел

$\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e$ $\lim _{{x\to \infty }}\left(1+{\frac {1}{x}}\right)^{x}=e$ или $\lim _{x\to 0}\left(1+x\right)^{1/x}=e$ $\lim _{{x\to 0}}\left(1+x\right)^{{1/x}}=e$

Доказательство существования второго замечательного предела:

Доказательство для натуральных значений x

$\blacktriangleleft$ $\blacktriangleleft$ Докажем вначале теорему для случая последовательности $x_{n}=\left(1+{\frac {1}{n}}\right)^{n};\ n\in \mathbb {N}$ $x_{{n}}=\left(1+{\frac {1}{n}}\right)^{n};\ n\in {\mathbb N}$

По формуле бинома Ньютона : $(a+b)^{n}=a^{n}~+~{\frac {n}{1}}\cdot a^{n-1}\cdot b~+~{\frac {n(n-1)}{1\cdot 2}}\cdot a^{n-2}\cdot b^{2}~+~...~+~{\frac {n(n-1)(n-2)...(n-(n-1))}{1\cdot 2\cdot 3\cdot ...\cdot n}}\cdot b^{n};\ n\in \mathbb {N}$ $(a+b)^{n}=a^{n}~+~{\frac {n}{1}}\cdot a^{{n-1}}\cdot b~+~{\frac {n(n-1)}{1\cdot 2}}\cdot a^{{n-2}}\cdot b^{2}~+~...~+~{\frac {n(n-1)(n-2)...(n-(n-1))}{1\cdot 2\cdot 3\cdot ...\cdot n}}\cdot b^{n};\ n\in {\mathbb N}$

Полагая $a=1;~b={\frac {1}{n}}$ $a=1;~b={\frac {1}{n}}$ , получим:

\left(1+{\frac {1}{n}}\right)^{n}=1~+~{\frac {n}{1}}\cdot {\frac {1}{n}}~+~{\frac {n(n-1)}{1\cdot 2}}\cdot {\frac {1}{n^{2}}}~+~{\frac {n(n-1)(n-2)}{1\cdot 2\cdot 3}}\cdot {\frac {1}{n^{3}}}~+~...~+~{\frac {n(n-1)(n-2)...(n-(n-1))}{1\cdot 2\cdot 3\cdot ...\cdot n}}\cdot {\frac {1}{n^{n}}}=

\left(1+{\frac {1}{n}}\right)^{n}=1~+~{\frac {n}{1}}\cdot {\frac {1}{n}}~+~{\frac {n(n-1)}{1\cdot 2}}\cdot {\frac {1}{n^{2}}}~+~{\frac {n(n-1)(n-2)}{1\cdot 2\cdot 3}}\cdot {\frac {1}{n^{3}}}~+~...~+~{\frac {n(n-1)(n-2)...(n-(n-1))}{1\cdot 2\cdot 3\cdot ...\cdot n}}\cdot {\frac {1}{n^{n}}}=

=1~+~1~+~{\frac {1}{1\cdot 2}}\cdot \left(1-{\frac {1}{n}}\right)~+~{\frac {1}{1\cdot 2\cdot 3}}\cdot \left(1-{\frac {1}{n}}\right)\cdot \left(1-{\frac {2}{n}}\right)~+~...~+~{\frac {1}{1\cdot 2\cdot 3\cdot ...\cdot n}}\cdot \left(1-{\frac {1}{n}}\right)\cdot \left(1-{\frac {2}{n}}\right)\cdot ...\cdot \left(1-{\frac {n-1}{n}}\right)

=1~+~1~+~{\frac {1}{1\cdot 2}}\cdot \left(1-{\frac {1}{n}}\right)~+~{\frac {1}{1\cdot 2\cdot 3}}\cdot \left(1-{\frac {1}{n}}\right)\cdot \left(1-{\frac {2}{n}}\right)~+~...~+~{\frac {1}{1\cdot 2\cdot 3\cdot ...\cdot n}}\cdot \left(1-{\frac {1}{n}}\right)\cdot \left(1-{\frac {2}{n}}\right)\cdot ...\cdot \left(1-{\frac {n-1}{n}}\right)

(1)

С увеличением $n$ $n$ число положительных слагаемых в правой части равенства (1) увеличивается. Кроме того, при увеличении $n$ $n$ число ${\frac {1}{n}}$ ${\frac {1}{n}}$ убывает, поэтому величины $\left(1-{\frac {1}{n}}\right),\left(1-{\frac {2}{n}}\right),...$ $\left(1-{\frac {1}{n}}\right),\left(1-{\frac {2}{n}}\right),...$ возрастают. Поэтому последовательность $\{x_{n}\}=\left\{\left(1+{\frac {1}{n}}\right)^{n}\right\};\ n\in \mathbb {N}$ $\{x_{{n}}\}=\left\{\left(1+{\frac {1}{n}}\right)^{n}\right\};\ n\in {\mathbb N}$ — возрастающая , при этом

\left(1+{\frac {1}{n}}\right)^{n}\geq 2,n\in \mathbb {N}

\left(1+{\frac {1}{n}}\right)^{n}\geq 2,n\in \mathbb {N}

(2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

\left(1+{\frac {1}{n}}\right)^{n}<1+1+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}~+~...~+~{\frac {1}{1\cdot 2\cdot 3\cdot ...\cdot n}}

\left(1+{\frac {1}{n}}\right)^{n}<1+1+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}~+~...~+~{\frac {1}{1\cdot 2\cdot 3\cdot ...\cdot n}}

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

\left(1+{\frac {1}{n}}\right)^{n}<1+\left(1+{\frac {1}{2}}+{\frac {1}{2^{2}}}+...+{\frac {1}{2^{n-1}}}\right)

\left(1+{\frac {1}{n}}\right)^{n}<1+\left(1+{\frac {1}{2}}+{\frac {1}{2^{2}}}+...+{\frac {1}{2^{{n-1}}}}\right)

.

Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

1+{\frac {1}{2}}+{\frac {1}{2^{2}}}+...+{\frac {1}{2^{n-1}}}={\frac {1\cdot \left(1-({\frac {1}{2}})^{n}\right)}{1-{\frac {1}{2}}}}=2\cdot \left(1-{\frac {1}{2^{n}}}\right)<2

1+{\frac {1}{2}}+{\frac {1}{2^{2}}}+...+{\frac {1}{2^{{n-1}}}}={\frac {1\cdot \left(1-({\frac {1}{2}})^{n}\right)}{1-{\frac {1}{2}}}}=2\cdot \left(1-{\frac {1}{2^{n}}}\right)<2

.

Поэтому $\left(1+{\frac {1}{n}}\right)^{n}<1+2=3$ $\left(1+{\frac {1}{n}}\right)^{n}<1+2=3$ (3).

Итак, последовательность ограничена сверху, при этом $\forall n\in \mathbb {N}$ $\forall n\in {\mathbb N}$ выполняются неравенства (2) и (3): $2\leq \left(1+{\frac {1}{n}}\right)^{n}<3$ $2\leq \left(1+{\frac {1}{n}}\right)^{n}<3$ .

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность $x_{n}=\left(1+{\frac {1}{n}}\right)^{n},\ n\in \mathbb {N}$ $x_{{n}}=\left(1+{\frac {1}{n}}\right)^{n},\ n\in {\mathbb N}$ монотонно возрастает и ограничена, значит имеет предел, обозначаемый буквой e . Т.е. $\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e$ $\lim _{{n\to \infty }}\left(1+{\frac {1}{n}}\right)^{n}=e$ $\blacktriangleright$ $\blacktriangleright$

$\blacktriangleleft$ $\blacktriangleleft$ Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что $\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e;\ x\in \mathbb {R}$ $\lim _{{x\to \infty }}\left(1+{\frac {1}{x}}\right)^{x}=e;\ x\in {\mathbb R}$ . Рассмотрим два случая:

1. Пусть $x\rightarrow +\infty$ $x\rightarrow +\infty$ . Каждое значение x заключено между двумя положительными целыми числами: $n\leqslant x<n+1$ $n\leqslant x<n+1$ , где $n=[x]$ $n=[x]$ — это целая часть x.

Отсюда следует:

{\frac {1}{n+1}}<{\frac {1}{x}}\leqslant {\frac {1}{n}}~~\Longleftrightarrow ~~1+{\frac {1}{n+1}}<1+{\frac {1}{x}}\leqslant 1+{\frac {1}{n}}

{\frac {1}{n+1}}<{\frac {1}{x}}\leqslant {\frac {1}{n}}~~\Longleftrightarrow ~~1+{\frac {1}{n+1}}<1+{\frac {1}{x}}\leqslant 1+{\frac {1}{n}}

, поэтому

\left(1+{\frac {1}{n+1}}\right)^{n}<\left(1+{\frac {1}{x}}\right)^{x}\leqslant \left(1+{\frac {1}{n}}\right)^{n+1}

\left(1+{\frac {1}{n+1}}\right)^{n}<\left(1+{\frac {1}{x}}\right)^{x}\leqslant \left(1+{\frac {1}{n}}\right)^{n+1}

.

Если

x\rightarrow +\infty

x\rightarrow +\infty

, то

n\rightarrow \infty

n \rightarrow \infty

. Поэтому, согласно пределу

\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e

\lim _{{n\to \infty }}\left(1+{\frac {1}{n}}\right)^{n}=e

, имеем:

\lim _{n\to \infty }\left(1+{\frac {1}{n+1}}\right)^{n}={\frac {\lim \limits _{n\to \infty }(1+{\frac {1}{n+1}})^{n+1}}{\lim \limits _{n\to \infty }\left(1+{\frac {1}{n+1}}\right)}}={\frac {e}{1}}=e

\lim _{{n\to \infty }}\left(1+{\frac {1}{n+1}}\right)^{n}={\frac {\lim \limits _{{n\to \infty }}(1+{\frac {1}{n+1}})^{{n+1}}}{\lim \limits _{{n\to \infty }}\left(1+{\frac {1}{n+1}}\right)}}={\frac {e}{1}}=e

\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n+1}=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\cdot \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)=e\cdot 1=e

\lim _{{n\to \infty }}\left(1+{\frac {1}{n}}\right)^{{n+1}}=\lim _{{n\to \infty }}\left(1+{\frac {1}{n}}\right)^{n}\cdot \lim _{{n\to \infty }}\left(1+{\frac {1}{n}}\right)=e\cdot 1=e

.

По признаку (о пределе промежуточной функции) существования пределов

\lim _{x\to +\infty }\left(1+{\frac {1}{x}}\right)^{x}=e

\lim _{{x\to +\infty }}\left(1+{\frac {1}{x}}\right)^{x}=e

.

2 . Пусть $x\to -\infty$ $x\to -\infty$ . Сделаем подстановку $-x=t$ $-x=t$ , тогда

\lim _{x\to -\infty }\left(1+{\frac {1}{x}}\right)^{x}=\lim _{t\to +\infty }\left(1-{\frac {1}{t}}\right)^{-t}=\lim _{t\to +\infty }\left({\frac {t}{t-1}}\right)^{t}=\lim _{t\to +\infty }\left(1+{\frac {1}{t-1}}\right)^{t}=

\lim _{{x\to -\infty }}\left(1+{\frac {1}{x}}\right)^{x}=\lim _{{t\to +\infty }}\left(1-{\frac {1}{t}}\right)^{{-t}}=\lim _{{t\to +\infty }}\left({\frac {t}{t-1}}\right)^{t}=\lim _{{t\to +\infty }}\left(1+{\frac {1}{t-1}}\right)^{t}=

=\lim _{t\to +\infty }\left(1+{\frac {1}{t-1}}\right)^{t-1}\cdot \lim _{t\to +\infty }\left(1+{\frac {1}{t-1}}\right)^{1}=e\cdot 1=e

=\lim _{{t\to +\infty }}\left(1+{\frac {1}{t-1}}\right)^{{t-1}}\cdot \lim _{{t\to +\infty }}\left(1+{\frac {1}{t-1}}\right)^{1}=e\cdot 1=e

.

Очевидно, из двух этих случаев вытекает, что $\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e$ $\lim _{{x\to \infty }}\left(1+{\frac {1}{x}}\right)^{x}=e$ для вещественного x. $\blacktriangleright$ $\blacktriangleright$

Следствия

$\lim _{u\to 0}(1+u)^{\frac {1}{u}}=e$ $\lim _{{u\to 0}}(1+u)^{{\frac {1}{u}}}=e$
$\lim _{x\to \infty }\left(1+{\frac {k}{x}}\right)^{x}=e^{k}$ $\lim _{x\to \infty }\left(1+{\frac {k}{x}}\right)^{x}=e^{k}$
$\lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1$ $\lim _{{x\to 0}}{\frac {\ln(1+x)}{x}}=1$
$\lim _{x\to 0}{\frac {e^{x}-1}{x}}=1$ $\lim _{{x\to 0}}{\frac {e^{x}-1}{x}}=1$
$\lim _{x\to 0}{\frac {a^{x}-1}{x\ln a}}=1$ $\lim _{{x\to 0}}{\frac {a^{x}-1}{x\ln a}}=1$ для $a>0$ $a>0$ , $a\neq 1$ $a\neq 1$
$\lim _{x\to 0}{\frac {(1+x)^{\alpha }-1}{\alpha x}}=1$ $\lim _{{x\to 0}}{\frac {(1+x)^{\alpha }-1}{\alpha x}}=1$
$\lim _{x\to \infty }\left(1-{\frac {k}{x}}\right)^{x}=e^{-k}$ $\lim _{x\to \infty }\left(1-{\frac {k}{x}}\right)^{x}=e^{-k}$

Доказательства следствий

$\lim _{u\to 0}(1+u)^{\frac {1}{u}}=\left[{\begin{matrix}u=1/x\\x\to \infty \end{matrix}}\right]=\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e$ $\lim _{{u\to 0}}(1+u)^{{\frac {1}{u}}}=\left[{\begin{matrix}u=1/x\\x\to \infty \end{matrix}}\right]=\lim _{{x\to \infty }}\left(1+{\frac {1}{x}}\right)^{x}=e$
$\lim _{x\to \infty }\left(1+{\frac {k}{x}}\right)^{x}=\left[{\begin{matrix}u=x/k\\x=ku\\u\to \infty \\x\to \infty \end{matrix}}\right]=\lim _{u\to \infty }\left(1+{\frac {1}{u}}\right)^{ku}=\left(\lim _{u\to \infty }\left(1+{\frac {1}{u}}\right)^{u}\right)^{k}=e^{k}$ $\lim _{{x\to \infty }}\left(1+{\frac {k}{x}}\right)^{x}=\left[{\begin{matrix}u=x/k\\x=ku\\u\to \infty \\x\to \infty \end{matrix}}\right]=\lim _{{u\to \infty }}\left(1+{\frac {1}{u}}\right)^{{ku}}=\left(\lim _{{u\to \infty }}\left(1+{\frac {1}{u}}\right)^{u}\right)^{k}=e^{k}$
$\lim _{x\to 0}{\frac {\ln(1+x)}{x}}=\lim _{x\to 0}{\frac {1}{x}}\ln(1+x)=\lim _{x\to 0}\ln((1+x)^{\frac {1}{x}})=\ln e=1$ $\lim _{{x\to 0}}{\frac {\ln(1+x)}{x}}=\lim _{{x\to 0}}{\frac {1}{x}}\ln(1+x)=\lim _{{x\to 0}}\ln((1+x)^{{\frac {1}{x}}})=\ln e=1$
$\lim _{x\to 0}{\frac {e^{x}-1}{x}}=\left[{\begin{matrix}u=e^{x}-1\\x=\ln(1+u)\\x\to 0\\u\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {u}{\ln(1+u)}}=1$ $\lim _{{x\to 0}}{\frac {e^{x}-1}{x}}=\left[{\begin{matrix}u=e^{x}-1\\x=\ln(1+u)\\x\to 0\\u\to 0\end{matrix}}\right]=\lim _{{u\to 0}}{\frac {u}{\ln(1+u)}}=1$
$\lim _{x\to 0}{\frac {a^{x}-1}{x\ln a}}=\lim _{x\to 0}{\frac {e^{\ln(a^{x})}-1}{x\ln a}}=\lim _{x\to 0}{\frac {e^{x\ln a}-1}{x\ln a}}=\left[{\begin{matrix}u=x\ln a\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {e^{u}-1}{u}}=1$ $\lim _{{x\to 0}}{\frac {a^{x}-1}{x\ln a}}=\lim _{{x\to 0}}{\frac {e^{{\ln(a^{x})}}-1}{x\ln a}}=\lim _{{x\to 0}}{\frac {e^{{x\ln a}}-1}{x\ln a}}=\left[{\begin{matrix}u=x\ln a\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{{u\to 0}}{\frac {e^{u}-1}{u}}=1$
$\lim _{x\to 0}{\frac {(1+x)^{\alpha }-1}{\alpha x}}=\lim _{x\to 0}{\frac {e^{\alpha \ln(1+x)}-1}{\alpha x}}=\lim _{x\to 0}{\frac {e^{\alpha \ln(1+x)}-1}{\alpha \ln(1+x)}}\cdot \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=$ $\lim _{{x\to 0}}{\frac {(1+x)^{\alpha }-1}{\alpha x}}=\lim _{{x\to 0}}{\frac {e^{{\alpha \ln(1+x)}}-1}{\alpha x}}=\lim _{{x\to 0}}{\frac {e^{{\alpha \ln(1+x)}}-1}{\alpha \ln(1+x)}}\cdot \lim _{{x\to 0}}{\frac {\ln(1+x)}{x}}=$