Interested Article - Периметр

Периметр — длина контура замкнутой плоской фигуры, длина границы.

Пери́метр ( др.-греч. περίμετρον — окружность , др.-греч. περιμετρέο — измеряю вокруг ) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина .

Иногда периметром называют границу геометрической фигуры.

Вычисление периметра имеет существенное практическое значение. Например, для вычисления длины ограды вокруг сада или участка. Периметр колеса (окружности) определяет, насколько далеко оно продвинется при полном обороте. Таким же образом, длина нитки, намотанной на катушку, тесно связана с периметром катушки.

Формулы

фигура	формула	переменные
окружность	$2\pi r=\pi d$ $2\pi r=\pi d$	где $r$ $r$ — радиус окружности, а $d$ $d$ — диаметр .
треугольник	$a+b+c$ $a+b+c$	где $a$ $a$ , $b$ $b$ и $c$ $c$ — длины сторон треугольника.
квадрат / ромб	$4a$ $4a$	где $a$ $a$ — длина стороны.
прямоугольник	$2(l+w)$ $2(l+w)$	где $l$ $l$ — длина (основания), а $w$ $w$ — ширина.
равносторонний многоугольник	$n\times a$ $n\times a$	где $n$ $n$ — число сторон, а $a$ $a$ — длина сторон.
правильный многоугольник	$2nb\sin \left({\frac {\pi }{n}}\right)$ $2nb\sin \left({\frac {\pi }{n}}\right)$	где $n$ $n$ — число сторон, а $b$ $b$ — расстояние от центра многоугольника до одной из вершин многоугольника.
общий многоугольник	$a_{1}+a_{2}+a_{3}+\cdots +a_{n}=\sum _{i=1}^{n}a_{i}$ $a_{1}+a_{2}+a_{3}+\cdots +a_{n}=\sum _{i=1}^{n}a_{i}$	где $a_{i}$ $a_{{i}}$ — длина $i$ $i$ -й (1, 2, 3 ... n ) стороны n -угольника.

Многоугольники

Многоугольники являются основными фигурами для определения периметров, и не только потому, что они являются простейшими фигурами, но и потому, что периметры многих фигур вычисляются путём аппроксимации их последовательностью многоугольников. Первым известным математиком, который использовал этот подход, был Архимед , который аппроксимировал периметр окружности путём описывания около неё правильных многоугольников .

Периметр многоугольника равен сумме длин его сторон. В частности, периметр прямоугольника , имеющего ширину $w$ $w$ и длину $\ell$ $\ell$ , равен $2w+2\ell$ $2w+2\ell$ .

Равносторонний многоугольник — это многоугольник, имеющий равные длины сторон (например ромб — это равносторонний многоугольник с 4 сторонами). Чтобы вычислить периметр равностороннего многоугольника, нужно умножить число сторон на общую длину стороны.

Периметр правильного многоугольника можно вычислить по числу сторон и его радиусу , то есть расстоянию от центра до вершин. Длину стороны можно вычислить, используя тригонометрию . Если R — радиус многоугольника, а n — число сторон, периметр равен

2nR\sin \left({\frac {180^{\circ }}{n}}\right).

2nR\sin \left({\frac {180^{\circ }}{n}}\right).

Периметр окружности

Если диаметр окружности равен 1, её периметр равен π.

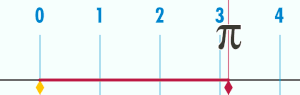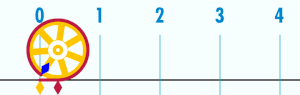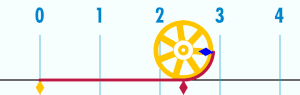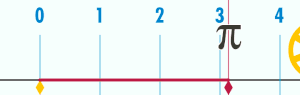
Периметр окружности пропорционален её диаметру (и радиусу ). То есть, существует константа π такая, что если P — периметр окружности, а D — её диаметр, то:

P=\pi \cdot {D}.

P=\pi \cdot {D}.

Для радиуса r окружности формула превращается в

{P}={2}\pi \cdot {r}.

{P}={2}\pi \cdot {r}.

Для вычисления периметра окружности знание радиуса или диаметра и числа π достаточно. Проблема заключается в том, что π не является рациональным (его нельзя выразить в виде дроби двух целых чисел ) и даже не является алгебраическим (оно не является корнем никакого полиномиального уравнения с рациональными коэффициентами). Таким образом, получение точного приближения к π важно для вычислений. Нахождение знаков π относится ко многим областям, таким как математический анализ и теория алгоритмов .

Осмысление периметра

Чем мельче структура фигуры, тем меньше площадь и тем больше периметр. Выпуклая оболочка остаётся той же самой.

Периметр крепости Нёф-Бризах сложный. Кратчайший путь для обхода крепости — по границе выпуклой оболочки .

Периметр и площадь являются двумя основными измерениями геометрических фигур, их часто ^{[

насколько?

]} путают ^{[

кто?

]} . Нередко также считают ^{[

кто?

]} , что увеличение одной из этих величин приводит к увеличению другой. Действительно, увеличение (или уменьшение) размера фигуры приводит к увеличению (или уменьшению) её площади, так же как и её периметра. Так, например, если нарисовать карту поля в масштабе 1/10 000, действительные размеры периметра можно вычислить простым умножением на 10 000. Действительная площадь будет в 10 000 ² раз больше площади фигуры на карте.

Тем не менее, нет никакой связи между площадью и периметром фигур ^{[

источник не указан 530 дней

]} . Например, периметр прямоугольника шириной 0,001 и длиной 1000 чуть больше 2000, в то время, как периметр прямоугольника шириной 0,5 и длиной 2 равен 5. Площади обеих фигур равны 1.

Прокл (V-й век) писал, что греческие крестьяне делили поля, опираясь на периметры , однако урожай с поля пропорционален площади, а не периметру, и много наивных крестьян получали поля с большим периметром, но малой площадью.

Если удалить часть фигуры, её площадь уменьшится, а вот периметр может и не уменьшиться. В случае очень неправильных фигур некоторые могут спутать периметр с выпуклой оболочкой . Выпуклую оболочку визуально можно представить как резинку, натянутую вокруг фигуры. На рисунке слева все фигуры имеют одну выпуклую оболочку ( шестиугольник ).

Изопериметрическая задача

Изопериметрическая задача — это задача нахождения фигуры с максимальной площадью среди фигур, имеющих заданный периметр. Решение интуитивно — это окружность . В частности поэтому капли жира в бульоне имеют форму кружочков.

Задача выглядит простой, но строгое математическое доказательство сложно. Изопериметрическая задача иногда упрощается — найти четырёхугольник , треугольник или другую определённую фигуру с наибольшей площадью среди имеющих заданный периметр. Решение изопериметрической задачи для четырёхугольников — квадрат , для треугольников — правильный треугольник . В общем случае, многоугольник с n сторонами имеет максимальную площадь при заданном периметре, если он является правильным , что ближе к окружности по сравнению с неправильными многоугольниками.