Interested Article - Диффузия

Схема осмоса через полупроницаемую мембрану.

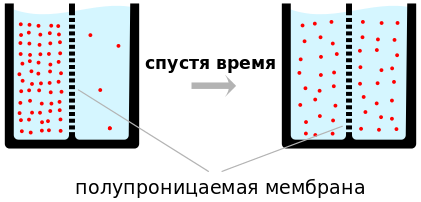
Диффу́зия ( лат. «распространение, растекание, рассеивание; взаимодействие») — неравновесный процесс перемещения (молекул и атомов в газах, ионов в плазме, электронов в полупроводниках и тому подобное) вещества из области с высокой концентрацией в область с низкой концентрацией, приводящий к самопроизвольному выравниванию концентраций по всему занимаемому объёму . Обычно рассматривают диффузию одного вещества в среде, но возможно и диффузия двух веществ, тогда говорят о взаимной диффузии газов. В плазме ионы и электроны имеют заряд и при взаимном проникновении одного вещества в другое вместо взаимной диффузии используют термин амбиполярная диффузия . При этом перенос вещества происходит из области с высокой концентрацией (или высоким химическим потенциалом) в область с низкой концентрацией (или низким химическим потенциалом) против направления градиента концентрации .

Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения.

Скорость протекания диффузии зависит от многих факторов. Так, в случае металлического стержня тепловая диффузия проходит с огромной скоростью. Если же стержень изготовлен из материала с низкой теплопроводностью (например, стекла), тепловая диффузия протекает медленно. Диффузия молекул в общем случае протекает ещё медленнее. Например, если кусочек сахара опустить на дно стакана с водой и воду не перемешивать, то пройдёт несколько недель, прежде чем раствор станет однородным. Ещё медленнее происходит диффузия одного твёрдого вещества в другое. Например, Роберт Бойль показал, что если медь покрыть золотом , то будет происходить диффузия золота в медь. При этом при нормальных условиях ( комнатная температура и атмосферное давление ) золотосодержащий слой достигнет толщины в несколько микронов только через несколько тысяч лет. Другой пример — систематические исследования диффузии свинца в золото, проведенные Уильямом Робертсом-Остеном и опубликованные в 1896 г. Под грузом за пять лет свинцовый слиток проник в золотой слиток на один миллиметр.

Первое систематическое экспериментальное исследование диффузии было выполнено Томасом Грэмом . Он изучал диффузию в газах, и это явление ( Закон Грэма ) было описано им в 1831—1833 гг.

Первое количественное описание процессов диффузии было дано немецким физиологом А. Фиком в 1855 году.

Большой вклад в теорию и практику исследования дифузионных процессов внес Я. И. Френкель , предложив и развив в 1926 году идею диффузии локальных дефектов (вакансий и межузельных атомов).

Общее описание

Все виды диффузии подчиняются одним законам. Скорость диффузии пропорциональна площади поперечного сечения образца, а также разности концентраций , температур или зарядов (в случае относительно небольших величин этих параметров). Так, тепло будет в четыре раза быстрее распространяться через стержень диаметром в два сантиметра, чем через стержень диаметром в один сантиметр. Это тепло будет распространяться быстрее, если перепад температур на одном сантиметре будет 10 °C вместо 5 °C. Скорость диффузии пропорциональна также параметру, характеризующему конкретный материал. В случае тепловой диффузии этот параметр называется теплопроводность , в случае потока электрических зарядов — электропроводность . Количество вещества, которое диффундирует в течение определённого времени, и расстояние, проходимое диффундирующим веществом, пропорциональны квадратному корню продолжительности диффузии.

Диффузия представляет собой процесс на молекулярном уровне и определяется случайным характером движения отдельных молекул . Скорость диффузии в связи с этим пропорциональна средней скорости молекул. В случае газов средняя скорость малых молекул больше, а именно она обратно пропорциональна квадратному корню из массы молекулы и растёт с повышением температуры. Диффузионные процессы в твёрдых телах при высоких температурах часто находят практическое применение. Например, в определённых типах электронно-лучевых трубок ( ЭЛТ ) применяется металлический торий , продиффундировавший через металлический вольфрам при 2000 °C.

Если в смеси газов масса одной молекулы в четыре раза больше другой, то такая молекула передвигается в два раза медленнее по сравнению с её движением в чистом газе. Соответственно, скорость диффузии её также ниже. Эта разница в скорости диффузии лёгких и тяжёлых молекул применяется, чтобы разделять субстанции с различными молекулярными весами. В качестве примера можно привести разделение изотопов . Если газ, содержащий два изотопа, пропускать через пористую мембрану, более лёгкие изотопы проникают через мембрану быстрее, чем тяжёлые. Для лучшего разделения процесс производится в несколько этапов. Этот процесс широко применялся для разделения изотопов урана (отделение ²³⁵ U от основной массы ²³⁸ U). Поскольку такой способ разделения требует больших энергетических затрат, были развиты другие, более экономичные способы разделения. Например, широко развито применение термодиффузии в газовой среде. Газ, содержащий смесь изотопов, помещается в камеру, в которой поддерживается пространственный перепад (градиент) температур. При этом тяжёлые изотопы со временем концентрируются в холодной области.

История

С исторической перспективе, диффузия в твердых телах использовалась задолго до создания теории диффузии. Например, Плиний Старший ранее описывал процесс цементирования, при котором сталь производится из железа (Fe) посредством диффузии углерода. Другой пример, хорошо известный на протяжении многих веков, — это диффузия окраски витражей или фаянса и китайской керамике .

В современной науке первое систематическое экспериментальное исследование диффузии было выполнено Томасом Грэмом . Он изучал диффузию в газах, и главное явление было описано им в 1831—1833 гг.:

"… газы различной природы, при контакте, не располагаются в соответствии с их плотностью: наиболее тяжелые в нижней части и более легкие в верхней части, — они самопроизвольно диффундируют взаимно и в равной степени друг через друга, и поэтому остаются в едином состоянии смеси на произвольный срок ".

Измерения Грэма помогли Джеймсу Клерку Максвеллу получить в 1867 году коэффициент диффузии CO ₂ в воздухе с ошибкой менее 5 %.

В 1855 году Адольф Фик , 26-летний лектор по анатомии из Цюриха, предложил . Он использовал измерения Грэма, заявив, что его цель — «разработка фундаментального закона для диффузии в единственном элементе пространства». Он осознал глубокую аналогию между диффузией и проводимостью тепла или электричества, создав формализм, подобный закону Фурье для теплопроводности (1822 г.) и закону Ома для электрического тока (1827 г.).

Роберт Бойль продемонстрировал диффузию в твердых телах в 17 веке путем проникновения цинка в медную монету. Тем не менее диффузия в твердых телах систематически не изучалась до второй половины XIX века. Уильям Чандлер Робертс-Остен , известный британский металлург и бывший помощник Томаса Грэма, систематически изучал диффузию твердого тела на примере золота в свинце в 1896 году. :

«. . . Моя давняя заинтересованность в исследованиях Грэхема сделала обязанностью попытаться распространить его работу по диффузии жидкости на металлы».

В 1858 году Рудольф Клаузиус ввел понятие средней длины свободного пробега . В том же году Джеймс Клерк Максвелл разработал первую атомистическую теорию процессов переноса в газах. Современная атомистическая теория диффузии и броуновского движения была разработана Альбертом Эйнштейном , Марианом Смолуховским и Жаном Батистом Перреном . Людвиг Больцман при разработке атомистических основ макроскопических процессов переноса ввел уравнение Больцмана , которое более 140 лет служит математикам и физикам источником идей и проблем.

В 1920—1921 годах Дьёрдь де Хевеши измерил с помощью радиоизотопов . Он изучал самодиффузию радиоактивных изотопов свинца в жидком и твердом свинце.

Яков Френкель предложил и развил в 1926 году идею диффузии в кристаллах через локальные дефекты (вакансии и межузельные атомы). Он пришел к выводу, что процесс диффузии в конденсированных средах представляет собой множество элементарных скачков и квазихимических взаимодействий частиц и дефектов. Он ввел несколько механизмов диффузии и нашел константы скорости из экспериментальных данных.

Некоторое время спустя Карл Вагнер и Уолтер Х. Шоттки развили идеи Френкеля о механизмах диффузии. В настоящее время общепризнано, что атомные дефекты необходимы для диффузии в кристаллах.

Генри Эйринг , с коллегами применил свою теорию к квазиклассической модели диффузии Френкеля. Аналогия между реакционной кинетикой и диффузией привела к различным нелинейным обобщениям закона Фика.

Модели диффузии

Уравнения Фика

С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии . При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал $\mu$ $\mu$ , обусловливающий поддержание потока вещества. При этом поток частиц вещества $J$ $J$ пропорционален концентрации $C$ $C$ и градиенту химического потенциала:

J

J

~

-C\left({\frac {\partial \mu }{\partial x}}\right)_{p,T}.

-C\left({\frac {\partial \mu }{\partial x}}\right)_{p,T}.

Используя разложение химического потенциала по степеням концентрации, справедливое для газов и слабых растворов,

\mu

\mu

=

k_{B}T\ln C+\phi _{0}(T)+{\phi _{1}(T)}{C}+\ldots

k_{B}T\ln C+\phi _{0}(T)+{\phi _{1}(T)}{C}+\ldots

,

можно показать, что ведущий член в выражении для потока частиц

J=-D{\frac {\partial C}{\partial x}}

J=-D{\frac {\partial C}{\partial x}}

,

который показывает, что плотность потока вещества $J$ $J$ (измеренная, например, в моль·см ⁻² с ⁻¹ ) пропорциональна коэффициенту диффузии $D$ $D$ [см ² ·с ⁻¹ ] и градиенту концентрации. Это уравнение выражает первый закон Фика. Второй закон Фика связывает пространственное и временно́е изменения концентрации ( уравнение диффузии ):

{\frac {\partial C}{\partial t}}={\partial \over \partial x}\left(D{\frac {\partial C}{\partial x}}\right)

{\frac {\partial C}{\partial t}}={\partial \over \partial x}\left(D{\frac {\partial C}{\partial x}}\right)

.

Коэффициент диффузии $D$ $D$ зависит от температуры. В ряде случаев в широком интервале температур эта зависимость представляет собой соотношение Эйнштейна .

Дополнительное поле, наложенное параллельно градиенту химического потенциала, нарушает стационарное состояние . В этом случае диффузионные процессы описываются нелинейным уравнением Фоккера — Планка . Процессы диффузии имеют большое значение в природе:

питание, дыхание животных и растений;
проникновение кислорода из крови в ткани человека.

Геометрическое описание уравнения Фика

Во втором уравнении Фика в левой части стоит скорость изменения концентрации во времени, а в правой части уравнения — вторая частная производная, которая выражает пространственное распределение концентрации, в частности, выпуклость функции распределения температуры, проецируемую на ось $x$ $x$ .

Уравнения Онсагера для многокомпонентной диффузии и термодиффузии

Законы Фика применимы для случая малых значений концентраций $n$ $n$ и градиентов концентрации $-\nabla n$ $-\nabla n$ .

В 1931 году Ларс Онсагер предложил модель для описания процессов переноса многокомпонентной среды в случае линейных термодинамических неравновесных систем:

\mathbf {J} _{i}=\sum _{j}L_{ij}X_{j}\,.

\mathbf {J} _{i}=\sum _{j}L_{ij}X_{j}\,.

Здесь $\mathbf {J} _{i}$ ${\mathbf {J}}_{i}$ — поток i -й компоненты и $X_{j}$ $X_{j}$ — термодинамическая сила , $L_{ij}$ $L_{{ij}}$ — матрица кинетических коэффициентов.

Термодинамическая сила по Онсагеру определяется как градиент от частной производной энтропии (термин «сила» Онсагер брал в кавычки, поскольку здесь подразумевается «движущая сила»):

X_{i}=\nabla {\frac {\partial s(n)}{\partial n_{i}}}\ ,

X_{i}=\nabla {\frac {\partial s(n)}{\partial n_{i}}}\ ,

где $n_{i}$ $n_{i}$ — «термодинамические координаты». Для тепло- и массопереноса мы можем положить $n_{0}=u$ $n_{0}=u$ (плотность внутренней энергии) и $n_{i}$ $n_{i}$ это концентрация $i$ $i$ -ой компоненты. Соответствующее значение движущих сил в таком случае выражаются следующим образом:

X_{0}={\rm {grad}}{\frac {1}{T}}\ ,\;\;\;X_{i}=-{\rm {grad}}{\frac {\mu _{i}}{T}}\;(i>0),

X_{0}={{\rm {grad}}}{\frac {1}{T}}\ ,\;\;\;X_{i}=-{{\rm {grad}}}{\frac {\mu _{i}}{T}}\;(i>0),

поскольку

{\rm {d}}s={\frac {1}{T}}{\rm {d}}u-\sum _{i\geq 1}{\frac {\mu _{i}}{T}}{\rm {d}}n_{i}.

{\rm {d}}s={\frac {1}{T}}{\rm {d}}u-\sum _{i\geq 1}{\frac {\mu _{i}}{T}}{\rm {d}}n_{i}.

Здесь $T$ $T$ — температура и $\mu _{i}$ $\mu _{i}$ — химический потенциал i -й компоненты. Следует отметить, что данное рассмотрение приводится без учёта движения среды, поэтому мы здесь пренебрегаем членом с производной давления. Такое рассмотрение возможно в случае малых концентраций примесей с малыми градиентами.

В линейном приближении вблизи точки равновесия мы можем выразить термодинамические силы следующим образом:

X_{i}=\sum _{k\geq 0}\left.{\frac {\partial ^{2}s(n)}{\partial n_{i}\partial n_{k}}}\right|_{n=n^{*}}{\rm {grad}}\,n_{k}\ ,

X_{i}=\sum _{k\geq 0}\left.{\frac {\partial ^{2}s(n)}{\partial n_{i}\partial n_{k}}}\right|_{n=n^{*}}{\rm {grad}}\,n_{k}\ ,

Матрица кинетических коэффициентов $L_{ij}$ $L_{{ij}}$ должна быть симметричной ( Теорема Онсагера ) и положительно определённой ( в случае роста энтропии ).

Транспортное уравнение в таком случае может быть записано в следующем виде:

{\frac {\partial n_{i}}{\partial t}}=-{\rm {div}}\mathbf {J} _{i}=-\sum _{j\geq 0}L_{ij}{\rm {div}}X_{j}=\sum _{k\geq 0}\left[-\sum _{j\geq 0}L_{ij}\left.{\frac {\partial ^{2}s(n)}{\partial n_{j}\partial n_{k}}}\right|_{n=n^{*}}\right]\Delta n_{k}\ .

{\frac {\partial n_{i}}{\partial t}}=-{{\rm {div}}}{\mathbf {J}}_{i}=-\sum _{{j\geq 0}}L_{{ij}}{{\rm {div}}}X_{j}=\sum _{{k\geq 0}}\left[-\sum _{{j\geq 0}}L_{{ij}}\left.{\frac {\partial ^{2}s(n)}{\partial n_{j}\partial n_{k}}}\right|_{{n=n^{*}}}\right]\Delta n_{k}\ .

Здесь индексы $i,~j,~k=0,1,2...$ $i,~j,~k=0,1,2...$ относятся к внутренней энергии (0) и разным компонентам. Выражение в квадратных скобках является матрицей $D_{ik}$ $D_{{ik}}$ диффузионных( $i,~k>0$ $i,~k>0$ ), термодиффузионных ( $i>0$ $i>0$ , $k=0\lor k>0,~i=0$ $k=0\lor k>0,~i=0$ ) и температуропроводных ( $i=k=0$ $i=k=0$ ) коэффициентов.

В изотермическом случае ( $T=const$ $T=const$ ) и термодинамический потенциал выражается через свободную энергию (или (англ.) (). Термодинамическая движущая сила для изотермичной диффузии определяется отрицательным градиентом химического потенциала $-(1/T)\nabla \mu _{j}$ $-(1/T)\nabla \mu _{j}$ , и матрица диффузионных коэффициентов выглядит следующим образом:

D_{ik}={\frac {1}{T}}\sum _{j\geq 1}L_{ij}\left.{\frac {\partial \mu _{j}(n,T)}{\partial n_{k}}}\right|_{n=n^{*}}

D_{{ik}}={\frac {1}{T}}\sum _{{j\geq 1}}L_{{ij}}\left.{\frac {\partial \mu _{j}(n,T)}{\partial n_{k}}}\right|_{{n=n^{*}}}

( $i,~k>0$ $i,~k>0$ ).

Существует произвол в выборе определения для термодинамических сил и кинетических коэффициентов, поскольку мы не можем измерить их отдельно, а только их комбинацию $\sum _{j}L_{ij}X_{j}$ $\sum _{j}L_{{ij}}X_{j}$ . Например, в оригинальной работе Онсагер использовал дополнительный множитель ( $T$ $T$ ), тогда как в курсе теоретической физики Ландау и Лифшица этот множитель отсутствует и сила имеет противоположный знак. Это различие можно учесть в формулах для вывода коэффициентов так, что они не повлияют на результаты измерения.

Недиагональная диффузия должна быть нелинейной

Формализм линейной необратимой термодинамики (Онсагера) генерирует систему линейных уравнений диффузии в виде

{\frac {\partial n_{i}}{\partial t}}=\sum _{j}D_{ij}\Delta c_{j}\,.

{\frac {\partial n_{i}}{\partial t}}=\sum _{j}D_{ij}\Delta c_{j}\,.

Если матрица коэффициентов диффузии диагональна, то эта система уравнений является лишь системой независимых уравнений Фика для различных компонент. Предположим, что диффузия не является диагональной, например, $D_{12}\neq 0$ $D_{12}\neq 0$ , и рассмотрим состояние, в котором $c_{2}=\ldots =c_{n}=0$ $c_{2}=\ldots =c_{n}=0$ . В этом состоянии $\partial n_{2}/\partial t=D_{12}\Delta n_{1}$ $\partial n_{2}/\partial t=D_{12}\Delta n_{1}$ . Если в некоторой точке $D_{12}\Delta n_{1}(x)<0$ $D_{12}\Delta n_{1}(x)<0$ то $n_{2}(x)$ $n_{2}(x)$ в течение короткого времени становится отрицательным в этой точке. Поэтому линейная недиагональная диффузии не сохраняет положительность концентраций. Недиагональные уравнения многокомпонентной диффузии должны быть нелинейными .

См. также

Примечания

Д. П. Зубарев. // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров . — М. : Советская энциклопедия , 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — 707 с. — 100 000 экз.
Бокштейн Б. С. Атомы блуждают по кристаллу. — Библиотека Квант. — М. : Наука, 1984. — Т. 28. — С. 9—11. — 209 с.
↑ L.W. Barr (1997), In: Diffusion in Materials, DIMAT 96 , ed. H.Mehrer, Chr. Herzig, N.A. Stolwijk, H. Bracht, Scitec Publications, Vol.1, pp. 1-9.
H. Mehrer. Heroes and Highlights in the History of Diffusion // Diffusion Fundamentals. — 2009. — Т. 11 , № 1 . — С. 1–32 .
↑ Diffusion Processes , Thomas Graham Symposium, ed. J.N. Sherwood, A.V. Chadwick, W.M.Muir, F.L. Swinton, Gordon and Breach, London, 1971.
↑ , p. 1—32.
Тамм И. Е. // Успехи физических наук . — 1962. — Т. LXXVI , № 3 . — С. 414 . 1 апреля 2014 года.
J. Philibert (2005). от 13 декабря 2013 на Wayback Machine Diffusion Fundamentals, 2, 1.1-1.10.
S. Chapman, T. G. Cowling (1970) The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases , Cambridge University Press (3rd edition), ISBN 052140844X .
J.F. Kincaid (1941). “The theory of absolute reaction rates and its application to viscosity and diffusion in the liquid State”. Chem. Rev . 28 (2): 301—65. DOI : .
↑ , H.P. Sargsyan and H.A. Wahab (2011). “Quasichemical Models of Multicomponent Nonlinear Diffusion”. Mathematical Modelling of Natural Phenomena . 6 (5): 184—262. arXiv : . DOI : .
↑ Onsager L. Reciprocal Relations in Irreversible Processes. I (англ.) // Physical Review : journal. — 1931. — Vol. 37 , no. 4 . — P. 405—426 . — doi : . — Bibcode : .
Ландау Л. Д. , Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М. : Физматлит , 2005. — 616 с. — (« Теоретическая физика », том V). — ISBN 5-9221-0054-8 .