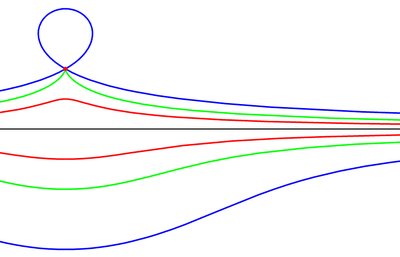
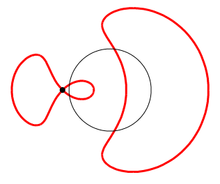
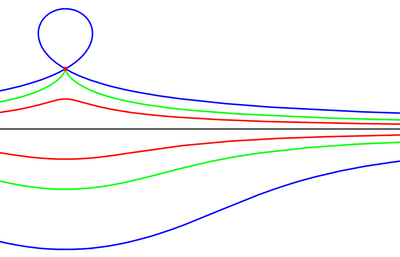
Конхоида Никомеда ― конхоида прямой, то есть кривая, получающаяся увеличением (вторая ветвь — уменьшением) радиус-вектора точек прямой на некую постоянную величину ${\displaystyle \ell }$ ; плоская алгебраическая кривая 4-го порядка. Конхоида имеет две ветви, сама прямая конхоиды является асимптотой обеих ветвей.

Название происходит от др.-греч. κογχοειδής — «похожий на раковину» .

Построение

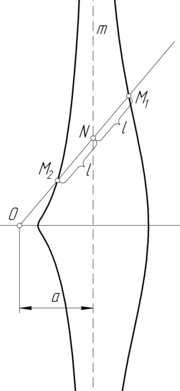
Пусть на плоскости выбрана прямая m и точка O , отстоящая от прямой на расстояние a . Проведём через точку O луч, пересекающий прямую m в некоторой точке N ; точки M ₁ и M ₂ , лежащие на луче ON и отстоящие от точки N на заранее выбранное расстояние l , будут точками конхоиды. Меняя направление луча ON , можно построить всю конхоиду .

Уравнения

Декартовы координаты

Если центр конхоиды помещён в начале координат , а прямая задана уравнением ${\displaystyle y+a=0}$ в декартовых прямоугольных координатах , то уравнение конхоиды имеет вид

${\displaystyle \ell ^{2}y^{2}=(x^{2}+y^{2})(y+a)^{2}}$

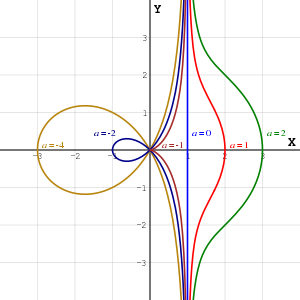
Начало координат является двойной точкой, характер которой зависит от величин ${\displaystyle a}$ и ${\displaystyle \ell }$ :

• при ${\displaystyle \ell <a}$ ― изолированная точка
• при ${\displaystyle \ell >a}$ ― узловая точка
• при ${\displaystyle \ell =a}$ ― точка возврата

Полярные координаты

В полярных координатах , если начало координат находится на расстоянии ${\displaystyle a}$ от прямой , которая смещается вдоль радиус-вектора на расстояние ${\displaystyle l}$ , уравнение конхоиды имеет вид

${\displaystyle r={\frac {a}{\cos \varphi }}\pm \ell .}$

История

Кривая названа по имени Никомеда (III—II века до н. э.), который применял её для решения задачи о трисекции угла и удвоения куба .

Примечания

Литература

• Прасолов В. В. . М.: Наука, 1992. 80 с. Серия «Популярные лекции по математике», выпуск 62.
• Савёлов А. А. Плоские кривые. Физматгиз, 1960.
• Конхоида // / Сост. А. П. Савин. — М. : Педагогика , 1985. — С. -151. — 352 с.