Правильный пятиугольник (или пентагон от греч. πενταγωνον ) — геометрическая фигура , правильный многоугольник с пятью сторонами.

Свойства

• У правильного пятиугольника угол равен

${\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}$

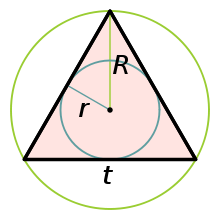
• Площадь правильного пятиугольника рассчитывается по любой из формул:

${\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}={\frac {5}{12}}Rd={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}}$ ,

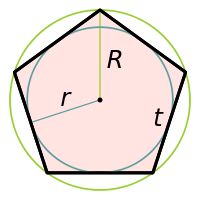
где ${\displaystyle R}$ — радиус описанной окружности , ${\displaystyle r}$ — радиус вписанной окружности, ${\displaystyle d}$ — диагональ , ${\displaystyle t}$ — сторона.

• Высота правильного пятиугольника:

${\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1{,}5388417685876268t}$

• Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению , то есть числу ${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$ .

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

• Сторона:

${\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}1755705045849463~R}$

• Радиус вписанной окружности:

${\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}6881909602355869~t}$

• Радиус описанной окружности:

${\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t\approx 0{,}85065080835204~t}$

• Диагональ:

${\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}9021130325903073~R\approx 1{,}618033988749895~t}$

• Площадь:

${\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}7204774005889671~t^{2}}$

• Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет )
• Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)

${\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}854101966249685}$

где ${\displaystyle \Phi }$ — отношение золотого сечения .

Построение

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность , или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O . (Это зелёная окружность на схеме справа).
2. Выберите на окружности точку A , которая будет одной из вершин пятиугольника. Постройте прямую через O и A .
3. Постройте прямую перпендикулярно прямой OA , проходящую через точку O . Обозначьте одно её пересечение с окружностью как точку B .
4. Постройте точку C посередине между O и B .
5. Проведите окружность с центром в точке C через точку A . Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D .
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F .
7. Проведите окружность с центром в E через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку G .
8. Проведите окружность с центром в F через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку H .
9. Постройте правильный пятиугольник AEGHF .

• Построение правильного пятиугольника
• 
  Построение правильного пятиугольника
• 
  Построение правильного пятиугольника
• 
  Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе

В природе не существует кристаллов с гранями в форме правильного пятиугольника, но исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры. Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская . Пентасимметрией обладают иглокожие (например морские звёзды ) и некоторые растения. См. также Закономерности в природе .

• 
  Иглокожие , например морские звёзды , обладают пентасимметрией
• 
  Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская

Интересные факты

В разделе не хватает ссылок на источники (см. рекомендации по поиску ). Информация должна быть проверяема , иначе она может быть удалена. Вы можете статью, добавив ссылки на авторитетные источники в виде сносок . ( 24 июля 2020 )

• Додекаэдр — единственный из правильных многогранников , грани которого представляют собой правильные пятиугольники.
• Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
• Правильный пятиугольник со всеми его диагоналями является проекцией правильного пятиячейника (4-симплекса).
• Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.

См. также

• Золотое сечение
• Пятиугольник
• Пентаэдр
• Пентаграмма
• Государственный знак качества СССР

Примечания