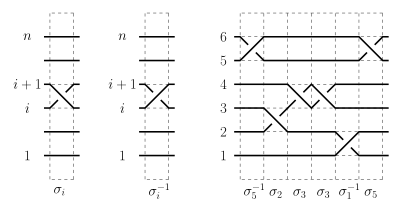
Произведение кос
Группа кос
—
группа
, образованная для заданного
n
{\displaystyle n}
всеми
косами
из
n
{\displaystyle n}
нитей относительно операции
произведения
кос. Является центральным объектом изучения
теории кос
и обозначается символом
B
n
{\displaystyle B_{n}}
.
Группа кос наделяется рядом
математических структур
, происходящих из
алгебры
,
комбинаторики
,
геометрии
и
топологии
, и допускает множество различных интерпретаций.
Группа
B
n
{\displaystyle B_{n}}
впервые явно описана
Эмилем Артином
в
1925 году
(см.
Теория кос § История
).
Определение
Группа кос имеет несколько различных воплощений, которые приводят к
изоморфным
группам. Ниже представлены основные такие воплощения, рассматриваемые в литературе.
Геометрические косы
Классический подход к определению группы кос основан на конструкции
умножения кос
. Так, произведением двух кос
α
{\displaystyle \alpha }
и
β
{\displaystyle \beta }
из одинакового числа нитей называется коса
α
β
{\displaystyle \alpha \beta }
, полученная путём соединения правых концов нитей первой косы с левыми концами нитей второй косы
.
Такое умножение задаёт на множестве
B
n
{\displaystyle B_{n}}
всех кос из
n
{\displaystyle n}
нитей
ассоциативную
бинарную операцию
.
Тривиальная коса
из
n
{\displaystyle n}
нитей, то есть такая, у которой все нити являются прямыми, является
нейтральным элементом
относительно умножения кос. Далее, все элементы из
B
n
{\displaystyle B_{n}}
обратимы относительно данной операции, а именно, обратным элементом к данному является
обратная коса
, которая получается из исходной косы отражением относительно плоскости, перпендикулярной её нитям
. Таким образом, вместе с операцией умножения множество
B
n
{\displaystyle B_{n}}
является
группой
, которая называется
группой кос
из
n
{\displaystyle n}
нитей
.
Данный подход к определению группы кос восходит к
теории узлов
.
Образующие Артина
, обратные к ним и коса, заданная некоторым
артиновским словом
Задание образующими и соотношениями
Согласно
теореме Артина
, группа кос порождается
образующими Артина
и допускает в этих образующих следующее конечное
задание
:
B
n
≅
⟨
σ
1
,
σ
2
,
…
,
σ
n
−
1
∣
σ
i
σ
i
+
1
σ
i
=
σ
i
+
1
σ
i
σ
i
+
1
{\displaystyle B_{n}\cong \langle \sigma _{1},\sigma _{2},\ldots ,\sigma _{n-1}\mid \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1}}
для
1
≤
i
≤
n
−
2
;
σ
i
σ
j
=
σ
j
σ
i
{\displaystyle 1\leq i\leq n-2;\ \ \sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}}
для
|
i
−
j
|
≥
2
⟩
{\displaystyle |i-j|\geq 2\rangle }
.
Данный изоморфизм предоставляет независимое определение группы кос, которое восходит к
комбинаторной теории групп
.
Траектории движения точек на плоскости
Группа кос может быть задана своим
, а именно, она изоморфна
фундаментальной группе
конфигурационного пространства
UConf
n
(
R
2
)
{\displaystyle \operatorname {UConf} _{n}(\mathbb {R} ^{2})}
неупорядоченных наборов
n
{\displaystyle n}
различных точек
евклидовой плоскости
:
B
n
≅
π
1
(
UConf
n
(
R
2
)
)
{\displaystyle B_{n}\cong \pi _{1}(\operatorname {UConf} _{n}(\mathbb {R} ^{2}))}
.
Данный изоморфизм предоставляет независимое определение группы кос, которое восходит к
теории гомотопий
.
Автоморфизмы свободной группы
Группа кос изоморфна группе
сплетающих автоморфизмов
свободной группы
.
Автогомеоморфизмы проколотого диска
Группа кос изоморфна
группе классов отображений
замкнутого
с
n
{\displaystyle n}
проколами
:
B
n
≅
M
o
d
(
D
n
2
;
∂
D
n
2
)
{\displaystyle B_{n}\cong {\rm {Mod}}(D_{n}^{2};\partial D_{n}^{2})}
.
Данный изоморфизм предоставляет независимое определение группы кос, которое восходит к
двумерной топологии
.
Свойства
Согласно
теореме Артина
, группы кос из малого числа нитей допускают следующие элементарные описания. Группа кос из одной нити
тривиальна
:
B
1
=
{
1
}
{\displaystyle B_{1}=\{1\}}
.
Группа кос из двух нитей является
бесконечной циклической
:
B
2
≅
⟨
σ
1
∣
∅
⟩
≅
Z
{\displaystyle B_{2}\cong \langle \sigma _{1}\mid \varnothing \rangle \cong \mathbb {Z} }
.
Группа кос из трёх нитей изоморфна
группе трилистника
:
B
3
≅
⟨
σ
1
,
σ
2
∣
σ
1
σ
2
σ
1
=
σ
2
σ
1
σ
2
⟩
{\displaystyle B_{3}\cong \langle \sigma _{1},\sigma _{2}\mid \sigma _{1}\sigma _{2}\sigma _{1}=\sigma _{2}\sigma _{1}\sigma _{2}\rangle }
.
При
n
≥
3
{\displaystyle n\geq 3}
ранг
группы кос
B
n
{\displaystyle B_{n}}
равен двум. Так, она не является циклической (и даже не является
абелевой
), но может быть порождена двумя элементами
σ
1
{\displaystyle \sigma _{1}}
и
σ
1
σ
2
…
σ
n
−
1
{\displaystyle \sigma _{1}\sigma _{2}\ldots \sigma _{n-1}}
.
Абелианизация и коммутант
При
n
≥
2
{\displaystyle n\geq 2}
абелианизация
группы кос
B
n
{\displaystyle B_{n}}
изоморфна бесконечной циклической группе
:
B
n
/
[
B
n
,
B
n
]
≅
Z
{\displaystyle B_{n}/[B_{n},B_{n}]\cong \mathbb {Z} }
.
Гомоморфизм абелианизации
B
n
→
Z
{\displaystyle B_{n}\to \mathbb {Z} }
сопоставляет косе
β
{\displaystyle \beta }
её
экспоненциальную сумму
e
x
p
(
β
)
{\displaystyle {\rm {exp}}(\beta )}
.
Таким образом,
коммутант
группы кос состоит из тех кос, у которых экспоненциальная сумма равна нулю:
[
B
n
,
B
n
]
=
{
β
∈
B
n
∣
e
x
p
(
β
)
=
0
}
{\displaystyle [B_{n},B_{n}]=\{\beta \in B_{n}\mid {\rm {exp}}(\beta )=0\}}
.
Например, группа
[
B
3
,
B
3
]
{\displaystyle [B_{3},B_{3}]}
является
свободной
ранга два с базисом
σ
2
σ
1
−
1
{\displaystyle \sigma _{2}\sigma _{1}^{-1}}
и
σ
1
σ
2
σ
1
−
2
{\displaystyle \sigma _{1}\sigma _{2}\sigma _{1}^{-2}}
.
Центр
Полный оборот лежит в центре группы кос
Центр
группы кос является циклическим. А именно, при
n
≥
3
{\displaystyle n\geq 3}
он порождается
полным оборотом
:
Z
(
B
n
)
=
⟨
Δ
n
2
⟩
{\displaystyle Z(B_{n})=\langle \Delta _{n}^{2}\rangle }
.
Кроме того,
Z
(
B
2
)
=
⟨
Δ
1
⟩
=
B
2
{\displaystyle Z(B_{2})=\langle \Delta _{1}\rangle =B_{2}}
.
Данное свойство позволяет установить, что при
n
≠
m
{\displaystyle n\neq m}
группы
B
n
{\displaystyle B_{n}}
и
B
m
{\displaystyle B_{m}}
не изоморфны
.
Автоморфизмы
Задача описания
автоморфизмов
группы кос была поставлена Эмилем Артином в 1947 году
и решена в 1981 году в работе
и
.
При
n
≥
2
{\displaystyle n\geq 2}
O
u
t
(
B
n
)
{\displaystyle {\rm {Out}}(B_{n})}
группы кос
B
n
{\displaystyle B_{n}}
является циклической и порождена классом
автоморфизма-отражения
τ
n
{\displaystyle \tau _{n}}
, действующего на
образующих Артина
формулой
σ
i
↦
σ
i
−
1
{\displaystyle \sigma _{i}\mapsto \sigma _{i}^{-1}}
.
Данный автоморфизм имеет порядок два, и имеется изоморфизм
O
u
t
(
B
n
)
≅
Z
/
2
Z
{\displaystyle {\rm {Out}}(B_{n})\cong \mathbb {Z} /2\mathbb {Z} }
.
Точная последовательность
1
→
I
n
n
(
B
n
)
→
A
u
t
(
B
n
)
→
O
u
t
(
B
n
)
→
1
{\displaystyle 1\to {\rm {Inn}}(B_{n})\to {\rm {Aut}}(B_{n})\to {\rm {Out}}(B_{n})\to 1}
расщепляется, и группа автоморфизмов группы кос раскладывается в
полупрямое произведение
:
A
u
t
(
B
n
)
≅
I
n
n
(
B
n
)
⋊
⟨
τ
n
⟩
{\displaystyle {\rm {Aut}}(B_{n})\cong {\rm {Inn}}(B_{n})\rtimes \langle \tau _{n}\rangle }
.
Группа внутренних автоморфизмов
I
n
n
(
B
n
)
{\displaystyle {\rm {Inn}}(B_{n})}
группы кос, будучи изоморфной её факторгруппе по центру, также изоморфна
группе классов отображений
сферы с
n
{\displaystyle n}
проколами:
I
n
n
(
B
n
)
≅
B
n
/
Z
(
B
n
)
≅
M
o
d
(
S
n
2
)
{\displaystyle {\rm {Inn}}(B_{n})\cong B_{n}/Z(B_{n})\cong {\rm {Mod}}(S_{n}^{2})}
.
Например, группа внутренних автоморфизмов группы кос из трёх нитей изоморфна
модулярной группе
:
I
n
n
(
B
3
)
≅
B
3
/
Z
(
B
3
)
≅
M
o
d
(
S
3
2
)
≅
P
S
L
2
(
Z
)
{\displaystyle {\rm {Inn}}(B_{3})\cong B_{3}/Z(B_{3})\cong {\rm {Mod}}(S_{3}^{2})\cong {\rm {PSL}}_{2}(\mathbb {Z} )}
.
Подводя итог, группа автоморфизмов группы кос изоморфна
расширенной
группе классов отображений сферы с
n
{\displaystyle n}
проколами:
A
u
t
(
B
n
)
≅
M
o
d
±
(
S
n
2
)
{\displaystyle {\rm {Aut}}(B_{n})\cong {\rm {Mod}}^{\pm }(S_{n}^{2})}
.
Кручение
При
n
≥
2
{\displaystyle n\geq 2}
группа кос не имеет
кручения
. Иными словами, любая коса, кроме тривиальной, имеет бесконечный порядок.
Одна из причин отсутствия кручения — наличие
линейных порядков
на группах кос
. Например,
порядка Деорнуа
.
Другая причина состоит в том, что фундаментальная группа любого
асферического
конечномерного CW-комплекса не имеет кручения, а конфигурационное пространство
UConf
n
(
R
2
)
{\displaystyle \operatorname {UConf} _{n}(\mathbb {R} ^{2})}
является асферическим
многообразием
.
Остаточная конечность и хопфовость
При
n
≥
2
{\displaystyle n\geq 2}
группа кос
B
n
{\displaystyle B_{n}}
является
остаточно конечной
. В частности, она
хопфова
.
Извлечение корней
Извлечение корней из кос однозначно с точностью до сопряженности
Для данных косы
β
∈
B
n
{\displaystyle \beta \in B_{n}}
и целого числа
m
{\displaystyle m}
задача определения того, существует ли коса
α
∈
B
n
{\displaystyle \alpha \in B_{n}}
со свойством
α
m
=
β
{\displaystyle \alpha ^{m}=\beta }
, алгоритмически разрешима. Но такая коса
α
{\displaystyle \alpha }
не обязательно единственна. Например, для любого
n
≥
2
{\displaystyle n\geq 2}
в группе кос
B
n
{\displaystyle B_{n}}
фундаментальная коса
Δ
n
2
{\displaystyle \Delta _{n}^{2}}
допускает следующие представления:
(
σ
1
σ
2
…
σ
n
−
1
)
n
=
(
σ
n
−
1
σ
n
−
2
…
σ
1
)
n
{\displaystyle (\sigma _{1}\sigma _{2}\ldots \sigma _{n-1})^{n}=(\sigma _{n-1}\sigma _{n-2}\ldots \sigma _{1})^{n}}
.
При
n
≥
3
{\displaystyle n\geq 3}
косы
σ
1
σ
2
…
σ
n
−
1
{\displaystyle \sigma _{1}\sigma _{2}\ldots \sigma _{n-1}}
и
σ
n
−
1
σ
n
−
2
…
σ
1
{\displaystyle \sigma _{n-1}\sigma _{n-2}\ldots \sigma _{1}}
различны, поскольку, например, различны
их перестановки
.
В сборнике открытых проблем комбинаторной теории групп
Геннадий Семёнович Маканин
сформулировал гипотезу о том, что любые два решения предыдущего уравнения сопряжены в группе кос. Вскоре, с помощью
, она была доказана
. Таким образом, извлечение корней из кос является однозначным
с точностью до сопряженности
.
Псевдохарактеры
При
n
≥
3
{\displaystyle n\geq 3}
пространство псевдохарактеров
группы кос
B
n
{\displaystyle B_{n}}
бесконечномерно
. Примечательный псевдохарактер на группе кос задаёт
закрученность косы
.
Линейность
При всех
n
≥
1
{\displaystyle n\geq 1}
группа кос
B
n
{\displaystyle B_{n}}
является
линейной
, то есть допускает
точное представление
в
полную линейную группу
над некоторым полем. Например,
является точным
.
Представление Бурау
, напротив, имеет нетривиальное ядро при всех
n
≥
5
{\displaystyle n\geq 5}
, но является точным при
n
≤
3
{\displaystyle n\leq 3}
, а вопрос о его точности при
n
=
4
{\displaystyle n=4}
остаётся открытым.
Подгруппы
Образующие Маркова группы крашеных кос
Группа крашеных кос
Множество всех
крашеных кос
из
n
{\displaystyle n}
нитей образует
нормальную подгруппу
группы кос
B
n
{\displaystyle B_{n}}
, которая обозначается символом
P
n
{\displaystyle P_{n}}
.
Для каждого
n
∈
N
{\displaystyle n\in \mathbb {N} }
группа
P
n
{\displaystyle P_{n}}
является
конечнопорождённой
, а именно, она порождается
n
(
n
−
1
)
/
2
{\displaystyle n(n-1)/2}
косами
A
i
,
j
:=
σ
j
−
1
σ
j
−
2
…
σ
i
+
1
σ
i
2
σ
i
+
1
−
1
…
σ
j
−
2
−
1
σ
j
−
1
−
1
,
{\displaystyle A_{i,j}:=\sigma _{j-1}\sigma _{j-2}\ldots \sigma _{i+1}\sigma _{i}^{2}\sigma _{i+1}^{-1}\ldots \sigma _{j-2}^{-1}\sigma _{j-1}^{-1},}
называющимися
образующими Маркова
, где
i
{\displaystyle i}
и
j
{\displaystyle j}
таковы, что
1
≤
i
<
j
≤
n
.
{\displaystyle 1\leq i<j\leq n.}
Факторгруппы
Симметрическая группа
Сопоставление
β
↦
π
β
{\displaystyle \beta \mapsto \pi _{\beta }}
косе
её перестановки
задаёт
групповой эпиморфизм
π
:
B
n
→
S
n
{\displaystyle \pi \colon B_{n}\to S_{n}}
из группы кос в
симметрическую группу
. Он переводит
образующие Артина
σ
i
{\displaystyle \sigma _{i}}
в элементарные
транспозиции
s
i
:=
(
i
,
i
+
1
)
{\displaystyle s_{i}:=(i,i+1)}
.
С помощью данного эпиморфизма косы из
n
{\displaystyle n}
нитей можно рассматривать как физический аналог
перестановок
множества
{
1
,
2
,
…
,
n
}
{\displaystyle \{1,2,\ldots ,n\}}
. Утверждение о том, что каждая коса представляется в виде произведения образующих Артина и их обратных, обобщает тот факт, что каждую перестановку можно представить в виде композиции транспозиций
s
i
{\displaystyle s_{i}}
. Принципиальное отличие состоит в том, что
σ
i
≠
σ
i
−
1
{\displaystyle \sigma _{i}\neq \sigma _{i}^{-1}}
, в то время как
s
i
=
s
i
−
1
{\displaystyle s_{i}=s_{i}^{-1}}
. Таким образом, грубо говоря, при описании косы в терминах элементарных транспозиций
(
i
,
i
+
1
)
{\displaystyle (i,i+1)}
необходимо задать не только индексы
i
{\displaystyle i}
, но то,
как именно
на этом участке нити под номерами
i
{\displaystyle i}
и
i
+
1
{\displaystyle i+1}
меняются местами — проходит первая или под второй. Игнорирование этой информации и приводит к понятию перестановки, соответствующей косе.
Ядром
эпиморфизма
π
{\displaystyle \pi }
является группа крашеных кос
P
n
{\displaystyle P_{n}}
. Согласно
теореме о гомоморфизме
,
B
n
/
P
n
≅
S
n
{\displaystyle B_{n}/P_{n}\cong S_{n}}
.
В частности, группа крашеных кос является
нормальной подгруппой
группы
B
n
{\displaystyle B_{n}}
индекса
n
!
{\displaystyle n!}
.
Усечённая группа кос
Для
n
,
m
∈
N
{\displaystyle n,m\in \mathbb {N} }
группа
B
n
(
m
)
{\displaystyle B_{n}(m)}
, заданная стандартными образующими и соотношениями группы кос
B
n
{\displaystyle B_{n}}
, а также дополнительной серией соотношений вида
σ
i
m
=
1
{\displaystyle \sigma _{i}^{m}=1}
для
1
≤
i
≤
n
−
1
,
{\displaystyle 1\leq i\leq n-1,}
называется
усечённой группой кос
.
Например, при
m
=
2
{\displaystyle m=2}
данное описание является стандартным заданием симметрической группы:
B
n
(
2
)
≅
S
n
{\displaystyle B_{n}(2)\cong S_{n}}
.
Две косы из
n
{\displaystyle n}
нитей имеют совпадающие образы относительно канонической проекции
B
n
→
B
n
(
m
)
{\displaystyle B_{n}\to B_{n}(m)}
в том и только том случае, если одну косу можно получить из другой конечной последовательностью
m
{\displaystyle m}
-преобразований (см.
Коса (математика) § Локальные преобразования кос
).
Как показал
Гарольд Коксетер
, при
n
,
m
≥
3
{\displaystyle n,m\geq 3}
группа
B
n
(
m
)
{\displaystyle B_{n}(m)}
конечна тогда и только тогда, когда
(
n
,
m
)
∈
{
(
3
,
3
)
,
(
3
,
4
)
,
(
3
,
5
)
,
(
4
,
3
)
,
(
5
,
3
)
}
{\displaystyle (n,m)\in \{(3,3),(3,4),(3,5),(4,3),(5,3)\}}
,
причем в этих случаях
порядок
группы
B
n
(
m
)
{\displaystyle B_{n}(m)}
равен, соответственно,
24
,
{\displaystyle 24,}
96
,
{\displaystyle 96,}
600
,
{\displaystyle 600,}
648
{\displaystyle 648}
и
155520.
{\displaystyle 155520.}
Группа гомотопических кос
Для
n
∈
N
{\displaystyle n\in \mathbb {N} }
группа
B
^
n
{\displaystyle {\hat {B}}_{n}}
, заданная стандартными образующими и соотношениями группы кос
B
n
{\displaystyle B_{n}}
, а также дополнительной бесконечной серией соотношений вида
[
A
j
,
k
,
g
A
j
,
k
g
−
1
]
=
1
{\displaystyle [A_{j,k},gA_{j,k}g^{-1}]=1}
для
1
≤
j
<
k
≤
n
{\displaystyle 1\leq j<k\leq n}
и элемента
g
{\displaystyle g}
подгруппы группы крашеных кос, порождённой элементами
A
1
,
k
,
A
2
,
k
,
…
,
A
k
−
1
,
k
,
{\displaystyle A_{1,k},A_{2,k},\ldots ,A_{k-1,k},}
где символ
[
x
,
y
]
:=
x
y
x
−
1
y
−
1
{\displaystyle [x,y]:=xyx^{-1}y^{-1}}
обозначает
коммутатор
элементов
x
{\displaystyle x}
и
y
{\displaystyle y}
, а символ
A
j
,
k
{\displaystyle A_{j,k}}
обозначает образующую Маркова группы крашеных кос, называется
группой гомотопических кос
.
Две косы из
n
{\displaystyle n}
нитей имеют совпадающие образы относительно канонической проекции
B
n
→
B
^
n
{\displaystyle B_{n}\to {\hat {B}}_{n}}
в том и только том случае, если они
гомотопны
.
См. также
Примечания
, p. 72.
, p. 10.
, p. 73.
, с. 18.
, p. 77.
, с. 49.
, с. 48.
, с. 57.
, с. 13.
↑
, с. 15.
, p. 30.
, с. 38.
, с. 40.
, p. 102.
.
, глава 7.
, с. 44.
, p. 37.
, Problem B11.
.
, p. 114.
, p. 125.
, p. 159.
, p. 79.
, p. 81.
, p. 110.
Литература
Сосинский, А. Б
.
(рус.)
. —
М.
:
МЦНМО
, 2001. — 24 с. — (Библиотека «Математическое просвещение»). —
ISBN 5-900916-76-6
.
.
// Математическое просвещение. —
М.
:
МЦНМО
, 2010. —
Т. 3
,
вып. 14
. —
С. 107–142
. —
ISBN 978-5-94057-597-9
.
Сосинский, А. Б
.
(рус.)
. —
М.
:
МЦНМО
, 2005. — 112 с. —
ISBN 5-94057-220-0
.
,
Тураев, В. Г
.
Группы кос = Braid groups
(рус.)
/ пер. с англ. С. Н. Малыгина. —
М.
:
МЦНМО
, 2014. — 424 с. —
ISBN 978-5-4439-0245-6
.
Прасолов, В. В
,
Сосинский, А. Б
.
Узлы, зацепления, косы и трёхмерные многообразия
(рус.)
. —
М.
:
МЦНМО
, 1997. — 352 с. —
ISBN 5-900916-10-3
.
Теория узлов
(рус.)
. — Москва-Ижевск: Институт компьютерных исследований, 2005. — 512 с. —
ISBN 5-93972-404-3
.
,
A Study of Braids. —
Springer
, 1999. — 277 с. — (Mathematics and Its Applications). —
ISBN 978-0-7923-5767-4
. —
doi
:
.
Ссылки
(англ.)
//
Annals of Mathematics
. — 1947. —
Vol. 48
,
no. 1
. —
P. 101–126
. —
doi
:
.
,
,
(англ.)
// Combinatorial and Geometric Group Theory. — Contemporary Mathematics, 2002. —
Vol. 296
,
iss. 2
. —
P. 1-38
. —
ISBN 978-0-8218-7886-6
. —
doi
:
.
. —
, 2003. —
№ 3
. —
С. 1103–1118
.
// Алгебра и анализ. — 2009. —
Т. 21
,
вып. 2
. —
С. 113—135
.
,
. —
American Journal of Mathematics
, 1981. —
Т. 103
,
№ 6
. —
С. 1151–1169
.
at
Contains extensive library for computations with
Braid
Groups
P. Fabel,
, Journal of Knot Theory and its Ramifications, Vol. 14, No. 8 (2005) 979—991
P. Fabel,
, Journal of Knot Theory and its Ramifications, Vol. 15, No. 1 (2006) 21-29
Группа кос
— статья из
Математической энциклопедии
. Чернавский А. В.
от 4 июня 2013 на
Wayback Machine
, моделирующее группу
B
5
.
C. Nayak and F. Wilczek’s connection of projective braid group representations to the fractional quantum Hall effect
от 5 октября 2018 на
Wayback Machine
Presentation for FradkinFest by C. V. Nayak
N. Read’s criticism of the reality of Wilczek-Nayak representation
от 5 октября 2018 на
Wayback Machine