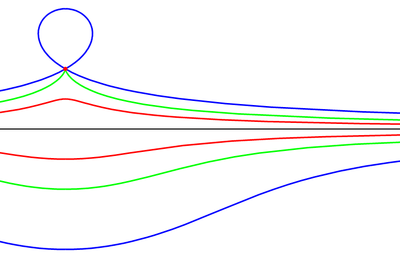
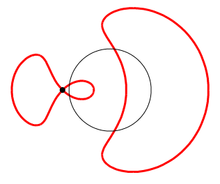
Конхоиды Слюза — это семейство плоских кривых , которые изучал в 1662 году Рене́-Франсу́а Валте́р , барон де Слюз .

Кривые задаются в полярных координатах уравнением

${\displaystyle r=\sec \theta +a\cos \theta }$ .

В декартовой системе кривые удовлетворяют уравнению

${\displaystyle (x-1)(x^{2}+y^{2})=ax^{2}}$

за исключением случая a = 0, в котором кривая имеет изолированную точку (0,0), которой нет в полярном представлении кривой.

Кривые являются рациональными , , кубическими плоскими кривыми .

Выражения имеют асимптоту x =1 (для a ≠0). Точка, наиболее удалённая от асимптоты — (1+ a ,0). (0,0) является для a <−1.

Для ${\displaystyle a\geq -1}$ область между кривой и асимптотой имеет площадь

${\displaystyle |a|(1+a/4)\pi }$

Для ${\displaystyle a<-1}$ площадь равна

${\displaystyle \left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}-a\left(2+{\frac {a}{2}}\right)\arcsin {\frac {1}{\sqrt {-a}}}.}$

Если ${\displaystyle a<-1}$ , кривая имеет петлю. Площадь петли равна

${\displaystyle \left(2+{\frac {a}{2}}\right)a\arccos {\frac {1}{\sqrt {-a}}}+\left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}.}$

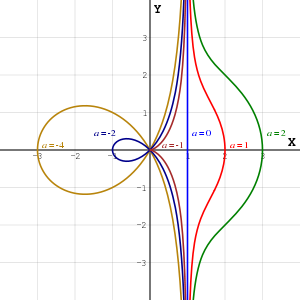
Четыре кривые из семейства имеют собственные имена:

a = 0, прямая (асимптота для остальных кривых семейства)

a = −1, циссоида Диокла

a = −2, правая строфоида

a = −4, трисектриса Маклорена

Примечания