Interested Article - Кривая Вивиани

Кривая Вивиани — пересечение сферы и цилиндра

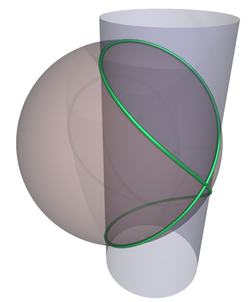
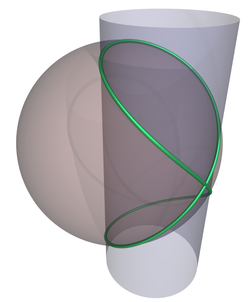
Кривая Вивиани — пространственная кривая, пересечение кругового цилиндра со сферой с центром на поверхности цилиндра и радиусом, равным диаметру цилиндра.

Названа в честь Винченцо Вивиани , который дал в 1692 году детальное исследование этой кривой и впервые отметил, что ограниченные ею на полусфере две области допускают простую квадратуру : их общая площадь такова, что поверхность оставшейся части полусферы равна площади квадрата, построенного на диаметре сферы . До Вивиани эту кривую изучали и Жиль Роберваль (1666).

Уравнения

Кривая Вивиани является линией пересечения поверхности цилиндра

$(x-a)^{2}+y^{2}=a^{2}$

со сферой вдвое большего радиуса, центр которой лежит на поверхности цилиндра:

x^{2}+y^{2}+z^{2}=4\cdot a^{2}\,.

Параметрическое уравнение:

$\left(a\cdot (1+\cos t),\ a\cdot \sin t,\ 2\cdot a\cdot \sin {\tfrac {t}{2}}\right).$

Уравнения проекций на плоскости $(x\,y)$ , $(y\,z)$ , $(x\,z)$ :

$x(z)=2\,r-{\dfrac {z^{2}}{2\,r}}\,,$

$y(z)=\pm z\,{\sqrt {1-{\dfrac {z^{2}}{4\,r^{2}}}}}\,,$

$y(x)=\pm {\sqrt {x(2\,r-x)}}\,,$

$z(x)=\pm {\sqrt {2\,r\,(2\,r-x)}}\,,$

$x(y)=r\pm {\sqrt {r^{2}-y^{2}}}\,,$

$z(y)=\pm {\sqrt {2\,r^{2}\pm 2\,r\,{\sqrt {r^{2}-y^{2}}}}}\,.$

Свойства

Проекция кривой Вивиани на общую касательную цилиндра и сферы является лемнискатой Жероно .
Кривая Вивиани на пересекающейся с цилиндром полусфере отделяет такие две области, что площадь оставшейся части полусферы равна площади квадрата, построенного на диаметре сферы.

Доказательство

Найдём площадь поверхности

f(x,y)={\sqrt {4\,r^{2}-x^{2}-y^{2}}}

, ограниченной кривой Вивиани, интегрированием в координатах

(x\,y)

.

Площадь поверхности определяется привычным образом через интеграл:

S_{\text{V.C.}}=\int \limits _{\Omega }{\sqrt {1+\left({\dfrac {\partial z}{\partial x}}\right)^{2}+\left({\dfrac {\partial z}{\partial y}}\right)^{2}}}\,\mathrm {d} x\,\mathrm {d} y\,,

где

\Omega

— область, ограниченная кривой Вивиани.

Вычислим подынтегральное выражение:

{\sqrt {1+\left({\dfrac {\partial z}{\partial x}}\right)^{2}+\left({\dfrac {\partial z}{\partial y}}\right)^{2}}}={\dfrac {2\,r}{\sqrt {4\,r^{2}-x^{2}-y^{2}}}}\,.

Продолжая вычисление и учитывая симметричность области интегрирования относительно оси

x\,

(получая таким образом четыре одинаковых части), находим:

S_{\text{V.C.}}=4\cdot 2\,r\,\int \limits _{0}^{2\,r}\mathrm {d} x\int \limits _{0}^{\sqrt {x\,(2\,r-x)}}\mathrm {d} y\,{\dfrac {1}{\sqrt {4\,r^{2}-x^{2}-y^{2}}}}=8\,r\int \limits _{0}^{2\,r}\mathrm {d} x\,\mathrm {arctg} {\sqrt {\dfrac {x}{2\,r}}}=8\,r\,(-2\,r+4\,r\,\mathrm {arctg} \,1)=8\,\pi \,r^{2}-16\,r^{2}={\dfrac {1}{2}}\,\pi \,(4\,r)^{2}-(4\,r)^{2}\,.

Первое слагаемое в получившемся выражении представляет собой площадь полусферы диаметра

4\,r

, второе слагаемое — площадь квадрата со стороной, равной этому же диаметру.

Таким образом, разность площадей полусферы и рассматриваемой поверхности равна площади квадрата, построенного на диаметре сферы:

S_{\text{hemisphere}}-S_{\text{V.C.}}=(4\,r)^{2}\,,

что и требовалось доказать.

Литература

Берже М. Геометрия, тт. 1—2. М: Мир, 1984.
Loria G. Curve sghembe speciali, Ed. Zanichelli, Bologna, 1925.
Roero C.S. L'intérêt international d'un problème proposé par Viviani, Actes de l’Univ. d'Été Hist. des Math., I.R.E.M. Toulouse, 1986.
Roero C.S. The Italian challange to Leibnitzian calculus in 1692. Leibnitz and Viviani: a comparison of two epistemologies, V Int. Congress Leibnitz, Hannover, 1988.