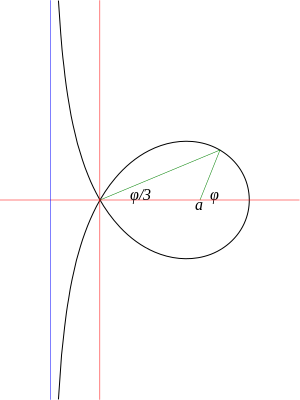
Трисектриса Маклорена — кубика , примечательная своим свойством трисекции , поскольку она может быть использована для трисекции угла. Её можно определить как геометрическое место точек пересечения двух прямых, каждая из которых вращаются равномерно вокруг двух различных точек (полюсов) с отношением угловых скоростей 1:3, при этом первоначально прямые совпадают с прямой, проходящей через эти полюса. Обобщение этого построения называется . Секущая названа в честь Колина Маклорена , который исследовал кривую в 1742 году.

Уравнения

Пусть две прямые вращаются вокруг точек ${\displaystyle P=(0,0)}$ и ${\displaystyle P_{1}=(a,0)}$ , так что прямая, вращающаяся вокруг ${\displaystyle P}$ , имеет с осью x угол ${\displaystyle \theta }$ , а вращающаяся вокруг ${\displaystyle P_{1}}$ , имеет угол ${\displaystyle 3\theta }$ . Пусть ${\displaystyle Q}$ — точка пересечения, тогда угол, образованный прямыми в точке ${\displaystyle Q}$ , равен ${\displaystyle 2\theta }$ . По теореме синусов

${\displaystyle {r \over \sin 3\theta }={a \over \sin 2\theta }}$ , так что в полярной системе координат это даст

${\displaystyle r=a{\frac {\sin 3\theta }{\sin 2\theta }}={a \over 2}{\frac {4\cos ^{2}\theta -1}{\cos \theta }}={a \over 2}(4\cos \theta -\sec \theta )}$ .

Таким образом, кривая принадлежит семейству конхоид Слюза .

В прямоугольной системе координат уравнение выглядит как

${\displaystyle 2x(x^{2}+y^{2})=a(3x^{2}-y^{2})}$ .

Если начало координат сдвинуть в ( a , 0), то вывод, близкий к приведённому, показывает, что уравнение в полярных координат превращается в

${\displaystyle r={\frac {a}{2\cos {\theta \over 3}}}}$

делая её примером .

Свойство трисекции

Для заданного угла ${\displaystyle \phi }$ рисуем луч из ${\displaystyle (a,0)}$ так, что угол с осью ${\displaystyle x}$ составляет ${\displaystyle \phi }$ . Рисуем луч из начала координат в точку пересечения первого луча с кривой. По построению кривой, угол между вторым лучом и осью ${\displaystyle x}$ равен ${\displaystyle \phi /3}$ .

Замечательные точки и свойства

Кривая имеет пересечение с осью x в точке ${\displaystyle 3a \over 2}$ и двойную неподвижную точку в начале координат. Вертикальная прямая ${\displaystyle x={-{a \over 2}}}$ является асимптотой. Кривая пересекает прямую ${\displaystyle x=a}$ в точках ${\displaystyle (a,{\pm {1 \over {\sqrt {3}}}a})}$ , соответствующих трисекции прямого угла. Как основная кубика, она имеет род нуль.

Связь с другими кривыми

Трисектриса Маклорена может быть определена как коническое сечение тремя путями. Конкретно:

• Она является инверсией гиперболы по отношению к единичной окружности

${\displaystyle 2x=a(3x^{2}-y^{2})}$ .

• Она является циссоидой окружности

${\displaystyle (x+a)^{2}+y^{2}=a^{2}}$

и прямой ${\displaystyle x={a \over 2}}$ относительно начала координат.

• Она является подерой параболы относительно начала координат

${\displaystyle y^{2}=2a(x-{\tfrac {3}{2}}a)}$ .

Вдобавок,

• Инверсия относительно точки ${\displaystyle (a,0)}$ является .
• Трисектриса Маклорена связана с декартовым листом аффинным преобразованием .

Литература

• J. Dennis Lawrence. . — Dover Publications, 1972. — С. , 95, 104—106 . — ISBN 0-486-60288-5 .
• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .

Ссылки