Interested Article - Многогранник Силаши

- 2021-06-16
- 1
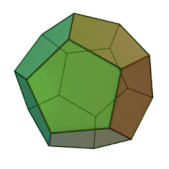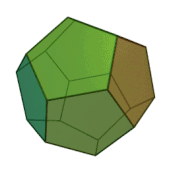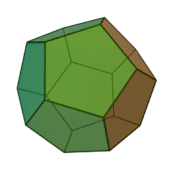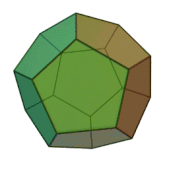
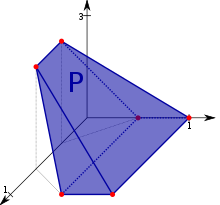
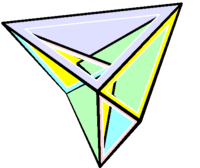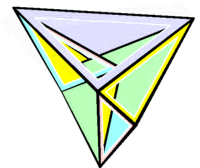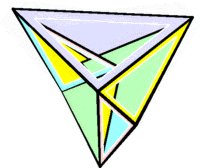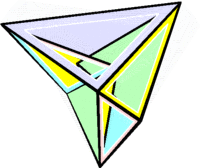
Многогранник Силаши ( Силашши ) — пример невыпуклого многогранника , топологически эквивалентного тору . Назван по имени венгерского математика , обнаружившего многогранник в 1977 году.
Свойства
- Имеет 7 шестиугольных граней.
-
Каждая грань этого многогранника имеет общее ребро с любой другой гранью.
- Как результат, для его правильной раскраски (чтобы смежные грани имели разные цвета) требуется семь цветов. Это даёт нижнюю оценку в .
- Многогранник имеет ось симметрии .
- Три пары граней попарно конгруэнтны , а одна непарная грань сама имеет вращательную симметрию, ту же самую, что и у многогранника.
- 14 вершин и 21 ребро многогранника Силаши образуют вложение графа Хивуда в поверхность тора.

-
Тетраэдр
и многогранник Силаши — единственные известные многогранники, у которых любые две грани имеют общее ребро.
-
Если многогранник с
f
гранями вложен в поверхность с
h
дырами таким образом, что каждые две грани имеют общее ребро, из
эйлеровой характеристики
следует, что
-
Если многогранник с
f
гранями вложен в поверхность с
h
дырами таким образом, что каждые две грани имеют общее ребро, из
эйлеровой характеристики
следует, что
-
- Это равенство выполняется для тетраэдра с h = 0 и f = 4 и для многогранника Силаши с h = 1 и f = 7. Следующее возможное решение с h = 6 и f = 12 могло бы соответствовать многограннику с 44 вершинами и 66 рёбрами, но неизвестно, существует ли такой многогранник. В общем случае это уравнение может выполняться только при f , сравнимом с 0, 3, 4 или 7 по модулю 12.
- Двойственный многограннику Силаши многогранник Часара был открыт в 1949 году . Он имеет семь вершин, 21 ребро, соединяющие каждую пару вершин, и 14 треугольных граней. Подобно многограннику Силаши, многогранник Часара имеет топологию тора.
В культуре
- В честь данного многогранника одна из московских школ назвала физико-математические классы «Силаэдр» [ неавторитетный источник ] .
- В математическом парке в городе Майкоп установлена скульптура такой формы .
Примечания
- ↑ . Дата обращения: 16 июня 2020. 16 июня 2020 года.
- .
- . Дата обращения: 16 июня 2020. 16 июня 2020 года.
- (2017). Дата обращения: 19 марта 2019. 30 июля 2020 года.
Литература
- Ákos Császár. A polyhedron without diagonals // Acta Sci. Math. Szeged. — 1949. — Т. 13 . — С. 140—142 .
- Martin Gardner . // Scientific American . — 1978. — Т. 239 , вып. 5 . — С. 22—32 . — doi : .
- M. Jungerman, Gerhard Ringel . Minimal triangulations on orientable surfaces // Acta Mathematica. — 1980. — Т. 145 , вып. 1–2 . — С. 121—154 . — doi : .
- Ivars Peterson. . — Mathematical Association of America , 2007.
- Lajos Szilassi. // Structural Topology. — 1986. — Т. 13 . — С. 69—80 .
- Клиффорд Пиковер. Великая математика. От Пифагора до 57-мерных объектов. 250 основных вех в истории математики = Clifford Alan Pickover. The Math Book. From Pythagoras to the 57th Dimension. 250 Milestones in the History of Mathematics / пер. с английского С. А. Иванова. — М. : Бином. Лаборатория знаний, 2014. — Гл. «1977 г. Многогранник Силаши». — ISBN 978-5-9963-0514-8 .
Ссылки
- Tom Ace. . .
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- — Papercraft model at
- 2021-06-16
- 1