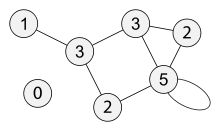
Степень ( валентность ) вершины графа — количество рёбер графа ${\displaystyle G}$ , инцидентных вершине ${\displaystyle x}$ . При подсчёте степени ребро- петля учитывается дважды.

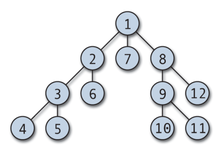
Степень вершины обычно обозначается как ${\displaystyle d(x)}$ или ${\displaystyle \deg(v)}$ . Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ( G ) и δ( G ). На рис. 1 максимальная степень равна 5, минимальная — 0. В регулярном графе степени всех вершин одинаковы, поэтому в данном случае можно говорить о степени графа .

Лемма о рукопожатиях

По формуле суммы степеней для графа ${\displaystyle G=(V,E)}$ ,

${\displaystyle \sum _{v\in V}\deg(v)=2|E|\,,}$

то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, из формулы следует, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях . Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других, чётно.

Последовательность степеней вершин

Последовательность степеней вершин неориентированного графа называется невозрастающая последовательность , образованная степенями всех вершин графа. Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа , так как у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристикой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.

Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической ( англ. graphical sequence). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа . Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары , к оставшимся незаполненными вершинам следует добавить петли.

Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность d _i (при i = 1,…, n ) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство

${\displaystyle \sum _{i=1}^{k}d_{i}\leq k(k-1)+\sum _{i=k+1}^{n}\min(d_{i},k)\quad \ k\in \{1,\dots ,n-1\}\,.}$

Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, но не при k равном 2 или 3.

Согласно критерию Гавела — Хакими , если невозрастающая последовательность ( d ₁ , d ₂ , …, d _n ) это последовательность степеней простого графа, то ( d ₂ − 1, d ₃ − 1, …, d _{d 1 +1} − 1, d _{d 1 +2} , d _{d 1 +3} , …, d _n ) некоторая последовательность степеней простого графа. Этот факт позволяет построить полиномиальный алгоритм нахождения простого графа с заданной реализуемой последовательностью.

Сопоставим исходной последовательности чисел вершины графа без ребер с требуемыми степенями. Указанное преобразование последовательностей задает как минимум одну вершину графа, все инцидентные ей ребра и множество вершин с новыми требуемыми дополнениями степеней. Упорядочивая оставшиеся вершины по невозрастанию дополнений степеней, получим невозрастающую последовательность степеней простого графа. Повторяя преобразование и упорядочение не более n-1 раза, получаем весь граф.

Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов .

Частные значения

• Вершина степени 0 называется изолированной .
• Вершина степени 1 называется концевой ( англ. end vertex), висячей ( англ. pendant vertex) или листом графа ( англ. leaf vertex). Ребро, инцидентное такой вершине называется висячим ( англ. terminal (pendant) edge, end-edge). На рис. 3 висячим ребром является {3,5}. Подобная терминология используется в изучении деревьев в общем и как структур данных .
• Вершина степени n-1 графа порядка n называется доминирующей ( англ. dominating vertex).

Общие свойства

• Если все вершины графа имеют одинаковую степень k , граф называют k -регулярным или регулярным графом степени k . В этом случае сам граф имеет степень k .
• Эйлеров путь существует в неориентированном, связном графе тогда и только тогда, когда граф имеет 0 или 2 вершины нечётной степени. Если граф содержит 0 вершин нечётной степени, Эйлеров путь является циклом.
• Орграф является псевдолесом ^{[ неизвестный термин ]} только если полустепень исхода каждой вершины не больше 1. Функциональный граф — частный случай псевдолеса, в котором полустепени исхода всех вершин равны 1.
• Согласно теореме Брукса, хроматическое число любого графа за исключением клики или нечётного цикла не превышает максимальной степени его вершин (Δ). Согласно теореме Визинга, хроматический индекс любого графа не превышает Δ + 1.
• k -вырожденным графом называется граф, в котором каждый подграф имеет вершину степенью не больше k .

См. также

• Полустепень захода и полустепень исхода вершин ориентированных графов
• Распределение степеней

Примечания

Источники

• Дистель, Рейнхард (2005), (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4 , < > .
• Эрдёш, П. & (1960), , Matematikai Lapok Т. 11: 264—274 , < > .
• (1962), On realizability of a set of integers as degrees of the vertices of a linear graph. I, Journal of the Т. 10: 496–506 .
• Сирксма, Хирард & Хоохефен, Хан (1991), , Т. 15 (2): 223–231 , DOI 10.1002/jgt.3190150209 .