Натуральный логарифм — логарифм по основанию e , где ${\displaystyle e}$ — трансцендентная константа, равная приблизительно 2,72. Он обозначается как ${\displaystyle \ln x}$ , ${\displaystyle \log _{e}x}$ или иногда просто ${\displaystyle \log x}$ , если основание ${\displaystyle e}$ подразумевается . Обычно число ${\displaystyle x}$ под знаком логарифма вещественное , но это понятие и на комплексные числа .

Из определения следует, что логарифмическая зависимость есть обратная функция для экспоненты ${\displaystyle y=e^{x}}$ , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (см. рисунок справа). Как и экспонента, логарифмическая функция относится к категории трансцендентных функций .

Натуральные логарифмы полезны для решения алгебраических уравнений , в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе .

В приложениях натуральный логарифм участвует в математическом описании таких процессов, в которых скорость изменения некоторого количества в каждый момент обратно пропорциональна самому количеству. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада радиоактивного вещества : чем больше атомов распадается, тем меньше их становится и тем медленнее идет дальнейший процесс. Натуральные логарифмы играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения различных задач, (например, нахождение сложных процентов ).

Определение

Натуральный логарифм числа ${\displaystyle a}$ — это показатель степени , в которую нужно возвести число e , чтобы получить ${\displaystyle a}$ . Другими словами, натуральный логарифм ${\displaystyle \ln a}$ есть решение ${\displaystyle x}$ уравнения ${\displaystyle e^{x}=a.}$

Примеры:

${\displaystyle \ln e=1}$ , потому что ${\displaystyle e^{1}=e}$ ;

${\displaystyle \ln 1=0}$ , потому что ${\displaystyle e^{0}=1}$ .

Вещественный натуральный логарифм

Натуральный логарифм ${\displaystyle \ln a}$ для вещественного числа ${\displaystyle a}$ определён и однозначен для любого положительного числа ${\displaystyle a.}$

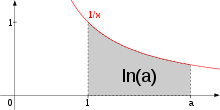
Натуральный логарифм может быть также определён геометрически для любого положительного вещественного числа a как площадь под кривой ${\displaystyle y={\frac {1}{x}}}$ на промежутке ${\displaystyle [1;a]}$ . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется данный логарифм, объясняет происхождение названия «натуральный».

Свойства

Из определения логарифма следует основное логарифмическое тождество :

${\displaystyle e^{\ln a}=a}$

Приведём сводку формул в предположении, что все значения положительны :

	Формула	Пример
Произведение	${\displaystyle \ln(xy)=\ln x+\ln y}$	${\displaystyle \ln(4\cdot 3)=\ln 4+\ln 3}$
Частное	${\displaystyle \ln \left({\frac {x}{y}}\right)=\ln x-\ln y}$	${\displaystyle \ln \left({\frac {1}{e^{2}}}\right)=\ln(1)-\ln(e^{2})=0-2=-2}$
Степень	${\displaystyle \ln(x^{p})=p\ln x}$	${\displaystyle \ln(64)=\ln(2^{6})=6\ln 2}$
Корень	${\displaystyle \ln {\sqrt[{p}]{x}}={\frac {\ln x}{p}}}$	${\displaystyle \ln {\sqrt {10}}={\frac {1}{2}}\ln 10}$

Другие свойства:

• Из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений.
• С возрастанием аргумента возрастает и логарифм: если ${\displaystyle 0<x<y,}$ то ${\displaystyle \ln x<\ln y.}$
• ${\displaystyle {\frac {h}{1+h}}\leqslant \ln(1+h)\leqslant h,}$ если ${\displaystyle h>-1.}$

Связь с логарифмами по другому основанию

Логарифм может быть определён для любого положительного основания, отличного от ${\displaystyle 1}$ , а не только для ${\displaystyle e}$ , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем.

Логарифм ${\displaystyle \log _{a}b}$ по основанию ${\displaystyle a}$ можно преобразовать в натуральный логарифм и обратно:

${\displaystyle \ln b={\frac {\log _{a}b}{\log _{a}e}}=\log _{a}b\cdot \ln a}$

${\displaystyle \log _{a}b={\frac {\ln b}{\ln a}}}$

Связь десятичного ( ${\displaystyle \lg x}$ ) и натурального логарифмов :

${\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}$

Связь двоичного ( ${\displaystyle \operatorname {lb} x}$ ) и натурального логарифмов:

${\displaystyle \ln x\approx 0,693147\operatorname {lb} x;\quad \operatorname {lb} x\approx 1{,}442695\ln x}$

Логарифмическая функция

Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию ${\displaystyle y=\ln x}$ . Она определена при ${\displaystyle x>0}$ . Область значений: ${\displaystyle E(y)=(-\infty ;+\infty)}$ . Эта кривая часто называется логарифмикой . Из формулы видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси ${\displaystyle y}$ ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.

Функция является строго возрастающей, она непрерывна и неограниченно дифференцируема всюду в своей области определения.

Ось ординат ( ${\displaystyle x=0}$ ) является вертикальной асимптотой , поскольку:

${\displaystyle \lim _{x\to 0+}\ln x=-\infty }$

Производная натуральной логарифмической функции равна:

${\displaystyle {\frac {d}{dx}}\ln x={\frac {1}{x}}}$

Простота этой формулы — одна из причин широкого использования именно натурального логарифма в анализе и при решении дифференциальных уравнений .

Проинтегрировав формулу для производной в интервале от ${\displaystyle x=1}$ до ${\displaystyle x=b}$ , мы получаем:

${\displaystyle \ln b=\int \limits _{1}^{b}{\frac {dx}{x}}}$

Другими словами, натуральный логарифм ${\displaystyle \ln {b}}$ равен площади под гиперболой ${\displaystyle y={\frac {1}{x}}}$ для указанного интервала ${\displaystyle [1,b]}$ .

С точки зрения общей алгебры , логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения :

${\displaystyle f(xy)=f(x)+f(y)}$

Аналитические свойства функции

Из формулы для производной натурального логарифма следует, что первообразная для гиперболы ${\displaystyle y=1/x}$ имеет вид:

${\displaystyle \int {dx \over x}=\ln |x|+C,}$

где ${\displaystyle C}$ — произвольная константа интегрирования. Поскольку функция ${\displaystyle y=1/x}$ состоит из двух ветвей (одна для положительных, другая для отрицательных ${\displaystyle x}$ ), семейство первообразных для ${\displaystyle y=1/x}$ тоже состоит из двух подсемейств, причём константы интегрирования у них независимы одна от другой.

Неопределённый интеграл от натурального логарифма легко найти интегрированием по частям :

${\displaystyle \int {\ln x\,\mathrm {d} x}=x\ln x-x+C}$

В математическом анализе и теории дифференциальных уравнений большую роль играет понятие логарифмической производной функции ${\displaystyle f(x)}$ :

${\displaystyle {\frac {d}{dx}}\ln(f(x))={\frac {f'(x)}{f(x)}}}$

Методы вычисления логарифма

Разложим натуральный логарифм в ряд Тейлора вблизи единицы:

${\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots }$

(Ряд 1)

Этот ряд, называемый « рядом Меркатора », сходится при ${\displaystyle -1<x\leqslant 1}$ . В частности:

${\displaystyle \ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots }$

Формула непригодна для практического расчёта логарифмов из-за того, что ряд сходится очень медленно и только в узком интервале. Однако нетрудно получить из неё более удобную формулу:

${\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)}$

(Ряд 2)

Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа ${\displaystyle z={\frac {1+x}{1-x}}}$ , ибо тогда ${\displaystyle x={\frac {z-1}{z+1}}}$ по абсолютной величине меньше единицы. Данный алгоритм уже пригоден для реальных численных расчётов значений логарифмов, однако не является наилучшим с точки зрения трудоёмкости.

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула: :

${\displaystyle \ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2}$

где ${\displaystyle M}$ обозначает арифметико-геометрическое среднее 1 и 4/s, и

${\displaystyle s=x\,2^{m}>2^{p/2},}$

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O( M ( n ) ln n ). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M ( n ) — вычислительная сложность умножения двух n -значных чисел.

Полезные пределы

Приведём несколько полезных пределов , связанных с логарифмами :

${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1}$

${\displaystyle \lim _{x\to 0+}x^{b}\ln x=0\quad (b>0)}$

${\displaystyle \lim _{x\to \infty }{\frac {\ln x}{x^{b}}}=0\quad (b>0)}$

${\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}$

${\displaystyle \ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}}$

Трансцендентность

Из теоремы Линдемана — Вейерштрасса (1885) вытекает следующее следствие: если аргумент ${\displaystyle x}$ есть алгебраическое число , отличное от единицы, то значение ${\displaystyle \ln x}$ есть не только иррациональное , но и трансцендентное число .

Непрерывные дроби

Хотя для представления логарифма отсутствуют классические непрерывные дроби , но можно использовать несколько «обобщённых непрерывных дробей», в том числе:

${\displaystyle \ln(1+x)={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\dots ={\cfrac {x}{1-0\cdot x+{\cfrac {1^{2}x}{2-1\cdot x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}}$

${\displaystyle \ln \left(1+{\frac {2x}{y}}\right)={\cfrac {2x}{y+{\cfrac {x}{1+{\cfrac {x}{3y+{\cfrac {2x}{1+{\cfrac {2x}{5y+{\cfrac {3x}{1+\ddots }}}}}}}}}}}}={\cfrac {2x}{y+x-{\cfrac {(1x)^{2}}{3(y+x)-{\cfrac {(2x)^{2}}{5(y+x)-{\cfrac {(3x)^{2}}{7(y+x)-\ddots }}}}}}}}}$

История

Впервые натуральные логарифмы в современном понимании появились в 1619 году, когда лондонский учитель математики Джон Спайдел переиздал логарифмические таблицы Непера , исправленные и дополненные так, что они фактически стали таблицами натуральных логарифмов . В 1649 году бельгийский математик Грегуар де Сен-Венсан показал, что площадь под гиперболой ${\displaystyle y={\frac {1}{x}}}$ меняется по логарифмическому закону, и предложил называть этот вид логарифмов «гиперболическим» .

Термин «натуральный логарифм» ввели в употребление Пьетро Менголи (1659 год) и Николас Меркатор в фундаментальном труде «Logarithmotechnia» (1668) . Там же Меркатор описал разложение натурального логарифма в « ряд Меркатора ».

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли , однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма . Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером . Бернулли и Д’Аламбер считали, что следует определить ${\displaystyle \log(-x)=\log(x)}$ , в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число . Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной .

Комплексные логарифмы

Комплексный логарифм — аналитическая функция , получаемая распространением вещественного логарифма на всю комплексную плоскость (кроме нуля). В отличие от вещественного случая, функция комплексного логарифма многозначна .

Определение . Натуральный логарифм ${\displaystyle \mathrm {Ln} \,z}$ комплексного числа ${\displaystyle z}$ представляет собой решение ${\displaystyle w}$ уравнения ${\displaystyle e^{w}=z.}$

Ненулевое число ${\displaystyle z}$ можно представить в показательной форме:

${\displaystyle z=r\cdot e^{i(\varphi +2\pi k)}\;\;,}$ где ${\displaystyle k}$ — произвольное целое число

Тогда ${\displaystyle \mathrm {Ln} \,z}$ находится по формуле :

${\displaystyle \mathrm {Ln} \,z=\ln r+i\left(\varphi +2\pi k\right)}$

Здесь ${\displaystyle \ln \,r=\ln \,|z|}$ — вещественный логарифм. Отсюда вытекает:

Комплексный логарифм ${\displaystyle \mathrm {Ln} \,z}$ существует для любого ${\displaystyle z\neq 0}$ , и его вещественная часть определяется однозначно, в то время как мнимая часть имеет бесконечное множество значений, различающихся на целое кратное ${\displaystyle 2\pi .}$

Из формулы видно, что у одного и только одного из значений мнимая часть находится в интервале ${\displaystyle (-\pi ,\pi ]}$ . Это значение называется главным значением комплексного натурального логарифма . Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается ${\displaystyle \ln \,z}$ . Если ${\displaystyle z}$ — вещественное число, то главное значение его логарифма совпадает с обычным вещественным логарифмом.

Логарифм отрицательного числа находится по формуле :

${\displaystyle \mathrm {Ln} (-x)=\ln x+i\pi (2k+1)\qquad (x>0,\ k=0,\pm 1,\pm 2\dots)}$

Примеры:

${\displaystyle \ln(1)=0;\;\mathrm {Ln} (1)=2k\pi i}$

${\displaystyle \ln(-1)=i\pi ;\;\mathrm {Ln} (-1)=(2k+1)i\pi }$

${\displaystyle \ln(i)=i{\frac {\pi }{2}};\;\mathrm {Ln} (i)=i{\frac {4k+1}{2}}\pi }$

Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:

${\displaystyle i\pi =\ln(-1)=\ln((-i)^{2})=2\ln(-i)=2(-i\pi /2)=-i\pi }$ — явная ошибка.

Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ( ${\displaystyle k=-1}$ ). Причина ошибки — неосторожное использование свойства ${\displaystyle \log _{a}{(b^{p})}=p~\log _{a}b}$ , которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.

• Функции натурального логарифма на комплексной плоскости (главная ветвь)
• 
  ${\displaystyle z=Re(\ln(x+iy))|}$
• 
  ${\displaystyle z=Im(\ln(x+iy))|}$
• 
  ${\displaystyle z=|\ln(x+iy)|}$
• 
  Суперпозиция трёх предыдущих графиков

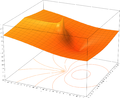
Функция натурального логарифма комплексного числа может быть также определена как аналитическое продолжение вещественного логарифма на всю комплексную плоскость , кроме нуля. Пусть кривая ${\displaystyle \Gamma }$ начинается в единице, заканчивается в z, не проходит через нуль и не пересекает отрицательную часть вещественной оси. Тогда главное значение логарифма в конечной точке ${\displaystyle w}$ кривой ${\displaystyle \Gamma }$ можно определить по формуле :

${\displaystyle \ln z=\int \limits _{\Gamma }{du \over u}}$

Некоторые применения

Теория чисел

Распределение простых чисел асимптотически подчиняется простым законам :

1. Число простых чисел в интервале от 1 до ${\displaystyle n}$ приблизительно равно ${\displaystyle {\frac {n}{\ln n}}}$ .
2. k -е простое число приблизительно равно ${\displaystyle k\ln k}$ .

Математический анализ

Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений . Примеры:

${\displaystyle \int {\operatorname {tg} x}\,dx=-\ln |\cos x|+C;\quad \int {\frac {dx}{\sqrt {x^{2}+a}}}=-\ln \ \left|\ x+{\sqrt {x^{2}+a}}\ \right|+C}$

Теория вероятностей и статистика

В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений. Например, логарифмическое распределение используется в генетике и физике. Логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных .

Для оценки неизвестного параметра широко применяются метод максимального правдоподобия и связанная с ним логарифмическая функция правдоподобия .

Флуктуации при случайном блуждании описывает закон Хинчина-Колмогорова .

Фракталы и размерность

Логарифмы помогают выразить размерность Хаусдорфа для фрактала . Например, рассмотрим треугольник Серпинского , который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое (см. рисунок). Размерность результата определяется по формуле:

${\displaystyle {\frac {\ln 3}{\ln 2}}\approx 1{,}58}$

Механика и физика

Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы , характеризующая степень её хаотичности .

Формула Циолковского применяется для расчёта скорости ракеты.

Химия и физическая химия

Уравнение Нернста связывает окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, а также со стандартными электродными потенциалами окислительно-восстановительных пар.

Логарифм используется в определениях таких величин, как показатель константы автопротолиза (самоионизации молекулы) и водородный показатель (кислотности раствора).

Психология и физиология

Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.

Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула — громкости звука , яркости света.

Закон Фиттса : чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется .

Время на принятие решения при наличии выбора можно оценить по .

Примечания

Литература

• Выгодский М. Я. . — М. : Наука, 1978.
  • Переиздание: АСТ, 2003, ISBN 5-17-009554-6 .
• Математика XVIII столетия // / Под редакцией А. П. Юшкевича , в трёх томах. — М. : Наука, 1972. — Т. III.
• Корн Г., Корн Т. . — М. : Наука, 1973. — 720 с.
• Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М. : Наука, 1967. — 304 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М. : Наука, 1966. — 680 с.

Ссылки

• " от 26 сентября 2013 на Wayback Machine " — перевод статьи (англ.)